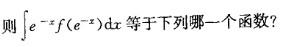参考答案和解析
正确答案:
由原方程F(x)G(x)=-1,两边对x求导得F′(x)G(x)+F(x)G′(x)=0。
又由于F(x)、G(x)分别是f(x)和1/f(x)的原函数,则F′(x)=f(x),G′(x)=1/f(x),且G(x)=-1/F(x)。
代入F′(x)G(x)+F(x)G′(x)=0,得-f(x)[1/F(x)]+F(x)[1/f(x)]=0,即[F(x)]2=[f(x)]2。
故F(x)=±f(x),F′(x)=±f′(x),即f′(x)=±f(x)。解得f(x)=C1ex及f(x)=C2e-x。
又f(0)=1,得C1=C2=1,则f(x)=e±x。
解析:
暂无解析
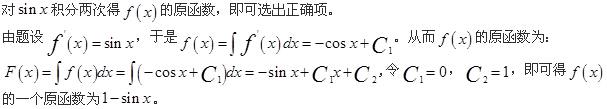
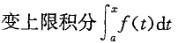 ,是下列中哪个函数?
,是下列中哪个函数?