x+ky+b=0
x+ky-b=0
x-ky-b=0
x-ky+b=0
第1题:
y关于x的线性回归方程为(作图),该回归直线必通过点( )。
A.(0,a)
B.(0,b)
C.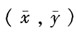
D.(a,b)
E.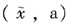
第2题:
在回归直线方程y=a+bx中,若a>0,下述正确的是
A、b>0
B、b<0
C、b=0
D、b=1
E、a的符号和b无关
第3题:
过点(2,1)且与直线y=0垂直的直线方程为 ( )
A.z=2
B.x=1
C.y=2
D.y=1
第4题:

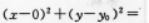 r2(如图)
r2(如图)


第5题:
 从而知直线//平面或直线与平面重合;再在直线上取一点(0,1,0),验证该点是否满足平面方程。
从而知直线//平面或直线与平面重合;再在直线上取一点(0,1,0),验证该点是否满足平面方程。第6题:
:直线y=kx+b(k≠0)与坐标轴交点的个数为( )。
A.1
B.2
C.0
D.1或2
因为y=kx+6,当b----0时为正比例函数只与坐标轴相交于原点即只有一个交点,当be=0时为一次函数应与x轴、Y轴分别有一个交点即此时有两个交点,因此答案为D。
第7题:
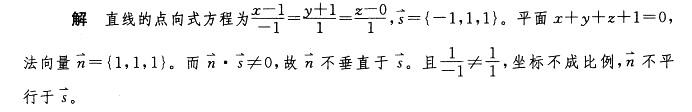
第8题:
直线z的方程为x-y-2=0,它关于点(1,-4)的对称直线方程为
A.x+y-8=0
B.x-y-8=0
C.z+y+8=0
D.x-y+8=0
第9题:
第10题: