两条不相交的直线
两条不平行的直线
不在同一平面内的两条直线
不在任何一个平面内的两条直线
第1题:
(15)对于四面体ABCD,下列命题正确的是_________(写出所有正确命题的编号)。
1相对棱AB与CD所在的直线异面;
2由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;
3若分别作 ABC和 ABD的边AB上的高,则这两条高所在的直线异面;
4分别作三组相对棱中点的连线,所得的三条线段相交于一点;
5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
解答:1,4,5
第2题:

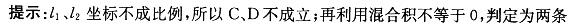
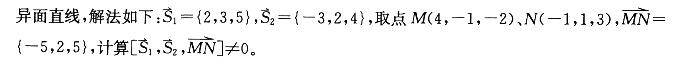
第3题:
过三棱柱任意两个顶点的直线共15条,其中异面直线有____________对。

第4题:
第5题:
第6题:
两条直线垂直于同一条直线,这两条直线的关系为( )
A.平行
B.相交
C.异面
D.位置不确定
第7题:
 则它们的关系是:
则它们的关系是:

第8题:
张老师在学生学了异面直线的定义后,提出如下命题并判断其正确性:
(1)在两个平面内的两条直线是异面直线;
(2)不在同一个平面内的两条直线是异面直线;
(3)不相交的两条直线是异面直线;
(4)不同在任何一个平面的两条直线是异面直线.
学生通过此类练习,对异面直线的定义中的“不同在任何一个平面的两条直线”的实质有了更深刻的认识.
仔细阅读案例,分析张老师运用了什么教学策略?结合自己的教学实践指出该教学策略运用的技巧.
第9题:
第10题: