违法和不良信息举报 联系客服
免费注册 登录

问答题某企业拟申请一项贷款用于项目改扩建，贷款额为1500万元，年利率为8%，贷款于年初一次发放。现有四种还款方案：方案一，自第一年起连续15年，每年年末等额偿还；方案二，自第一年起，每年年末偿还200万元；方案三，第六年年末偿还1000万元，其余款项于第十年年末一次支付；方案四，于第四年和第六年年末分别偿还600万元，剩余款项自第七年起四年内每年年末等额偿还。问题1．该企业若采用方案一，每年年末应偿还多少？2．该企业若采用方案二，可于几年内还清贷款？3．该企业若采用方案三，第十年年末应偿还的本息和为多少

题目
问答题
某企业拟申请一项贷款用于项目改扩建，贷款额为1500万元，年利率为8%，贷款于年初一次发放。现有四种还款方案：方案一，自第一年起连续15年，每年年末等额偿还；方案二，自第一年起，每年年末偿还200万元；方案三，第六年年末偿还1000万元，其余款项于第十年年末一次支付；方案四，于第四年和第六年年末分别偿还600万元，剩余款项自第七年起四年内每年年末等额偿还。问题1．该企业若采用方案一，每年年末应偿还多少？2．该企业若采用方案二，可于几年内还清贷款？3．该企业若采用方案三，第十年年末应偿还的本息和为多少？4．该企业若采用方案四，则第六至第十年应每年等额偿还多少？
如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

某工程项目建设期为 2 年，建设期内第 1 年初和第 2 年初分别贷款 600 万元和 400 万元，年利率为 8 ％。若运营期前 3 年每年末等额偿还贷款本息，到第 3 年末全部还清。则每年末应偿还贷款本息（ ）万元。

A ． 406.66

B ． 439.19

C ． 587.69

D ． 634.70


正确答案：B

第2题：

某企业向银行借贷资金为8万元，偿还期为4年，年利率10％，按复利计算，下列还款方式中，支付总金额最多的是()

A.每年年末偿还2万元本金和所欠利息
B.每年年末只偿还所欠利息，第4年年末一次还清本金
C.每年年末等额偿还
D.第4年年末一次还清本息

答案：D
解析：
复利是指在计算某一计息周期的利息时，其先前周期上所累积的利息要计算利息，即“利生利”、“利滚利”的计息方式。由其表达式：It=i×Ft-1可知，i一定时，Ft-1越大计算得到的It越大，所以在第4年年末一次还清本息是支付总金额最多的还款方式。

第3题：

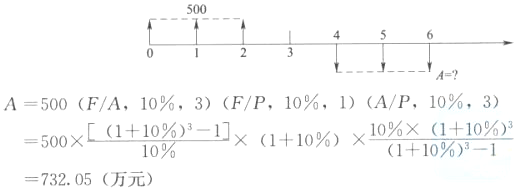
某项目建设期为2年，建设期内每年初贷款1000万元，年利率为8%。若运营期前5年每年末等额偿还贷款本息，到第5年末全部还清。则每年末偿还贷款本息()万元。

A.482.36

B.520.95

C.562.63

D.678.23


正确答案：C

第4题：

某企业向银行借入5年期贷款10000元，年利率10%，每年复利一次。则：
　　（1）若银行要求该企业在第5年末一次还清贷款，则企业预计的还款额是多少？
　　（2）若银行要求该企业在5年内，每年年末等额偿还该笔贷款，则企业预计每年年末的还款额是多少？


答案：
解析：
（1）第5年末一次还款额（复利终值F）＝10000×（F/P，10%，5）＝10000×1.6105＝16105（元）
　　（2）每年年末还款额（年资本回收额A）＝10000÷（P/A，10%，5）＝10000÷3.7908＝2637.97（元）

第5题：

某工程项目建设期为3年，建设期内每年初贷款500万元，年利率为10%。运营期前3年每年末等额偿还贷款本息，到第3年末全部还清。则每年末应偿还贷款本息（ ）万元。

A：606.83
B：665.50
C：732.05
D：953.60

答案：C
解析：
2019版教材P162
关于等值计算考核点，关键是理解等值计算的6个公式和有效利率与名义利率的概念与换算关系，并能灵活运用。历年在该考核点的考核形式万变不离其宗，考生可以针对本考核点多做一些练习题，以加快做题速度。
这一题其实很简单，因为借款是3年，还款也是3年，所以相当于把0、1、2期的借款，分别搬到了4、5、6期还款，所以就是500*1.1^4=732.05

第6题：

某企业获得一笔16万元的贷款，偿还期为8年，按年利率12%计复利，有5种还款方式：

(1)每年年末只偿还所欠利息，第八年年末一次还清本金；(2)在第八年年末一次还清本息，(3)在8年中每年年末等额偿还；(4)每年年末等额还本金，并付清当年的全部利息；(5)每年年末等额偿还本金，利息在第八年年末总付。试计算多种形式所付出的总金额。


正确答案：
(1)本金不变，所以每年偿还的利息为：160000×12%=19200(元)
8年共偿还金额为：160000+8×19200＝313600(元)
(2)第八年年末一次偿还本息：
F=160000×(1+12%)8=160000×2.476=396160(元)

8年共偿还金额为：8×32208=257664(元)
(4)每年等额偿还本金额：160000÷8=20000(元)
由于每年本金减少20000元，故每年利息减少20000×12%=2400(元)
第一年年末应偿还的利息为：160000×12%=19200(元)
第二年年末应偿还的利息为：19200-2400＝16800(元)
以此类推，第八年年末应偿还利息为：
19200-2400×7=2400(元)
故8年共偿还利息额为：
19200+16800+…+2400=86400(元)
所以8年共偿还金额为：
20000×8+86400=246400(元)

第7题：

某工程项目建设期为2年，建设期内第1年初和第2年初分别贷款600万元和400万元，年利率为8%。若运营期前3年每年末等额还贷款本息，到第3年末全部还清，则每年末应偿还本息（ ）万元。

A：406.66
B：439.19
C：587.69
D：634.70

答案：B
解析：
2019版教材P163
根据题意绘制现金流量图：则A=[600×（1+8%）^2+400×（1+8%）]×（A/P,8%,3）=439.19（万元）



也可以先把0期初的600和1期初的400折算到第5期末，这样可以求出F值，再由F求A
A=(600*1.08^5+400*1.08^4)*0.08/(1.08^3-1)

第8题：

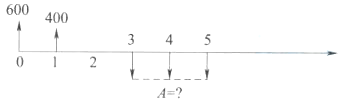
某项目建设期为2年，建设期内每年年初分别贷款600万元和900万元，年利率为10%。若在运营期前5年内于每年年末等额偿还贷款本利，则每年应偿还（ ）万元。

A．343.20

B．395.70

C．411.52

D．452.68


正确答案：D

第9题：

某企业年初从银行取得1000万元的贷款，8年期，年利率10%，现有以下几种还款方案：
方案一：每年年末等额偿还；
方案二：从第3年开始，每年年初等额偿还；
方案三：从第3年开始，每年年末等额偿还。
已知：（P/A，10%，8）＝5.3349，（P/A，10%，7）＝4.8684，（P/A，10%，6）＝4.3553，（P/F，10%，1）＝0.9091，（P/F，10%，2）＝0.8264
要求：
<1>?、分别计算各方案下还款年份每年应该偿还的金额。（结果保留两位小数）


答案：
解析：
（1）方案一表现为普通年金的形式
P＝A×（P/A，10%，8），A＝1000/5.3349＝187.44（万元）（1分）
（2）方案二从第3年开始每年年初等额偿还，表现为递延期为1年的递延年金，由于贷款期限为8年，所以，最后一次还款发生在第9年初（第8年末），共计还款7次。
P＝A×（P/A，10%，7）×（P/F，10%，1），A＝225.94（万元）（2分）
（3）方案三从第3年开始每年年末等额偿还，表现为递延期为2年的递延年金
P＝A×（P/A，10%，6）×（P/F，10%，2），A＝277.84（万元）（2分）

第10题：

某项目建设期为2年，建设期内每年初贷款1000万元，年利率为8%。若运营期前5年每年末等额偿还贷款本息，到第5年末全部还清。则每年末偿还贷款本息（ ） 万元。
A. 482.36 B. 520.95
C. 562.63 D. 678.23


答案：C
解析：
可画出现金流量表进行分析，把前两年的投资额折算至第二年末求出终值，再由此计算出题目要求的等额年值，计算周期为五年，故
1000CF/P, 8%, 2)+1000(F/P, 8%, 1)= 2246.4万元
A=P（A/P, i, n) = 2246.4(A/P，8%, 5) = 562.63
见教材第二章第一节P39
【考核要点】等值计算。

更多相关问题
相关内容