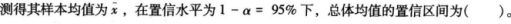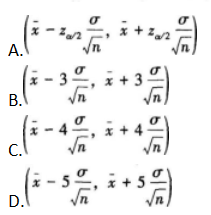A越大
B越小
C不变
第1题:
当出现以下( )情况,适合使用Z检验。
A.样本容量任意,但总体的标准差已知
B.样本容量任意,但总体的标准差未知
C.总体标准差未知,但样本容量>/=30。
D.总体标准差未知,但样本容量<30。
第2题:
已知总体服从正态分布,且总体标准差σ,从总体中抽取样本容量为n的产品,测得其样本均值为x,在置信水平为1-a=95%下,总体均值的置信区间为( )

第3题:
在估计某一总体均值时,随机抽取n个单元作样本,用样本均值作估计量,在构造置信区间时,发现置信区间太宽,其主要原因是( )。
A.样本容量太小
B.估计量缺乏有效性
C.选择的估计量有偏
D.抽取样本时破坏了随机性
第4题:

第5题:
研究者要估计某地区居民2013年的旅游支出。经验表明,总体标准差为5000元,如要求在95%的置信度水平下最大允许误差不超过500元,应该抽取的样本容量等于( )。(注:)
第6题:
A.样本要求的精确度越高,则样本容量就要越大
B.允许误差越大,样本容量就可以越小
C.总体异质性越高,则样本容量可以越小
D.总体同质性越高,则样本容量越大
E.总体规模越大,则样本容量越小
第7题:
在一个有限总体中,抽取样本容量为n的样本,其可能抽取的样本个数取决于( )。
A.样本容量的大小
B.总体全部单位数
C.抽样方法
D.抽样目的
E.总体方差
第8题:
从一个服从正态分布的总体中随机抽取样本容量为n的样本,在95%的置信度下对总体参数进行估计的结果为:20±0.08。如果其他条件不变,样本量扩大到原来的4倍,则总体参数的置信区间应该是( )。
A.20±0.16
B.20±0.04
C.80±0.16
D.80±0.04
第9题:
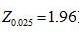 )
)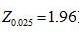
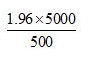

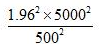
第10题: