
Aabecdf
Bacfebd
Caedfcb
Daebcfd
第1题:
A.非连通
B、连通
C、强连通
D、有向
第2题:
此题为判断题(对,错)。
第3题:
此题为判断题(对,错)。
第4题:
● 对连通图进行遍历前设置所有顶点的访问标志为 false(未被访问) ,遍历图后得到一个遍历序列,初始状态为空。深度优先遍历的含义是:从图中某个未被访问的顶点 v 出发开始遍历,先访问 v 并设置其访问标志为 true(已访问) ,同时将 v 加入遍历序列,再从 v 的未被访问的邻接顶点中选一个顶点,进行深度优先遍历;若 v的所有邻接点都已访问,则回到 v 在遍历序列的直接前驱顶点,再进行深度优先遍历,直至图中所有顶点被访问过。 (40) 是下图的深度优先遍历序列。
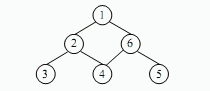
(40)
A. 1 2 3 4 6 5
B. 1 2 6 3 4 5
C. 1 6 2 5 4 3
D. 1 2 3 4 5 6
第5题:
此题为判断题(对,错)。
第6题:
已知一个图如图1.1所示,从顶点b出发进行广度优先遍历可能得到的序列为(23)。
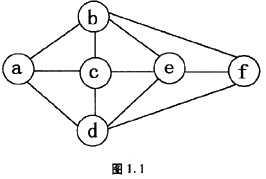
A.b a c e d f
B.b a c d f e
C.b a c e f d
D.b a c e f d
第7题:
此题为判断题(对,错)。
第8题:
阅读下列函数说明和C函数,将应填入(n)处的字句写在对应栏内。[说明]
邻接表是图的一种顺序存储与链式存储结合的存储方法。其思想是:对于图G中的每个顶点 vi,将所有邻接于vi的顶点vj连成一个单链表,这个单链表就称为顶点vi的邻接表,其中表头称作顶点表结点VertexNode,其余结点称作边表结点EdgeNode。将所有的顶点表结点放到数组中,就构成了图的邻接表AdjList。邻接表表示的形式描述如下: define MaxVerNum 100 /*最大顶点数为100*/
typedef struct node{ /*边表结点*/
int adjvex; /*邻接点域*/
struct node *next; /*指向下一个边表结点的指针域*/ }EdgeNode;
typedef struct vnode{ /*顶点表结点*/
int vertex; /*顶点域*/
EdgeNode *firstedge; /*边表头指针*/
}VertexNode;
typedef VertexNode AdjList[MaxVerNum]; /*AdjList是邻接表类型*/
typedef struct{
AdjList adjlist; /*邻接表*/
int n; /*顶点数*/
}ALGraph; /*ALGraph是以邻接表方式存储的图类型*/
深度优先搜索遍历类似于树的先根遍历,是树的先根遍历的推广。
下面的函数利用递归算法,对以邻接表形式存储的图进行深度优先搜索:设初始状态是图中所有顶点未曾被访问,算法从某顶点v出发,访问此顶点,然后依次从v的邻接点出发进行搜索,直至所有与v相连的顶点都被访问;若图中尚有顶点未被访问,则选取这样的一个点作起始点,重复上述过程,直至对图的搜索完成。程序中的整型数组visited[]的作用是标记顶点i是否已被访问。
[函数]
void DFSTraverseAL(ALGraph *G)/*深度优先搜索以邻接表存储的图G*/
{ int i;
for(i=0;i<(1);i++) visited[i]=0;
for(i=0;i<(1);i++)if((2)) DFSAL(G,i);
}
void DFSAL(ALGraph *G,int i) /*从Vi出发对邻接表存储的图G进行搜索*/
{ EdgeNode *p;
(3);
p=(4);
while(p!=NULL) /*依次搜索Vi的邻接点Vj*/
{ if(! visited[(5)]) DFSAL(G,(5));
p=p->next; /*找Vi的下一个邻接点*/
}
}
第9题:
设无向图G中的边的集合E={(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c)},则从顶点a出发进行深度优先遍历可以得到的一种顶点序列为()。
A.aedfcb
B.acfebd
C.aebcfd
D.aedfbc
第10题: