第1题：
已知数列{an}的前n项和Sn=n2-2n．求
（I）{an}的前三项；
（II）{an}的通项公式．
第2题：
已知数列{an}的通项公式为an =(4 9) n-1 - (2 3) n-1 (n ∈ N∗ ),则数列{an}( ).
(A)有最大项,没有最小项.
(B)有最小项,没有最大项.
(C)既有最大项又有最小项.
(D)既没有最大项也没有最小项.
第3题：
已知数列{an}满足an=3n+1(n为奇数，n∈N) 2n-2（n为偶数，n∈N）则a2·a3=（ ）。
A．70
B．28
C．20
D．8
第4题：
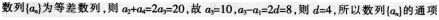
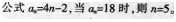
第5题：
设Sn为等差数列｛an｝的前n项和，若S3=3，S6=24，则a9= 。
第6题：
下面的程序是求菲波那契(Fibonacci)数列的前10项。已知该数列的前两项都为1，即F(1)=1，F(2)=1；而后面各项满足： F(n)=F(n-1)+F(n-2)。请在程序的每条横线处填写一条语句，使程序的功能完整。
注意：请勿改动main()主方法和其他已有的语句内容，仅在横线处填入适当的语句。
public class Fibonacci{
public static void main(String args[]){
System.out.printtn("Fibonacci is"+" "+"_______________________);
}
static long fib(int n){
if(______________)
return 1;
else
return _________________
}
}
第7题：
已知数列{an}中,a1=2,an+1=(1+an)/(1-an).记数列{an}的前n项的乘积为∏n,则∏2012=____.
第8题：
已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．
（I）求数列{an}的首项a1及通项公式；
（Ⅱ）数列{an}的前多少项的和等于847.
第9题：
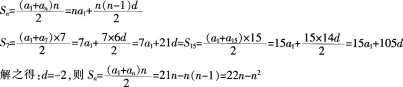
第10题：
两式相减得到a1 =3，因此数列前四项之和为3×（24-1）=45.