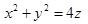平面的方程:
设平面II过点M0(x0,y0,zo),它的一个法向量n={A,B,C},平面II的方程为
A(x-x0)+B(y-y0)+C(z-z0)=0
此方程成为平面的点法式方程
平面的一般方程为Ax+By+Cz+D=0
期中n={A,B,C}为该平面的法向量
设一平面与轴分别交于P(a,0,0),Q(0,b,0)和R(0,0,c)三点(期中a≠0,b≠0,≠0),则该平面的方程为
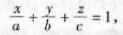
此方程称为平面的截距距式方程,a,b,c依次称为平面在x,y,z轴上的截距。
对于一些特殊的三元一次方程.应该熟悉它们的图形的特点如.在方程
Ax By+ Cz +D=0
中,当D=0时,方程表示一个通过原点的平面:当A=0时,方程表示一个平行于x轴的平面; 当A=B=0时,方程表示一个平行于xOy面的平面.类似地,可得其他情形的结论.
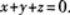

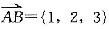 为直线的方向向量,直线的对称式方程为
为直线的方向向量,直线的对称式方程为 =
=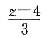


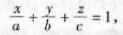 此方程称为平面的截距距式方程,a,b,c依次称为平面在x,y,z轴上的截距。
此方程称为平面的截距距式方程,a,b,c依次称为平面在x,y,z轴上的截距。