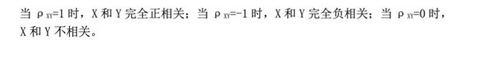第1题:
下列关于相关系数的说法中正确的是( )。
A.相关系数与协方差成正比关系
B.相关系数能反映证券之间的关联程度
C.相关系数为正,说明证券之间的走势相同
D.相关系数为1,说明证券之间是完全正相关关系
E.相关系数为0,说明证券之间不相关
第2题:
A.相关系数的取值范围在-1和+1之间
B. 相关系数的取值范围在0和+1之间
C. 相关系数的绝对值在0到1之间
D. 当相关系数等于 0.6时,说明两个变量之间是高度相关.
E. 相关系数的绝对值越接近于1,表示相关的程度越高
第3题:
A.市场组合的β值为1
B.市场组合的相关系数以及β值均为0
C.市场组合的相关系数为0
D.市场组合的相关系数以及β值均为1
E.市场组合的相关系数为1
第4题:
第5题:
下列叙述中,正确的是()。
A.若线性回归相关系数r=1,则两个变量线性无关
B.若线性回归相关系数r>0,当x增加时,y值增加
C.当相关系数r=1时,所有的实验点都落在回归线上
D.当相关系数r=0时,可能两个变量间有某种曲线的趋势
第6题:
A.Pearson和spearman 相关系数可以度量变量间线性相关的程度
B. 使用Pearson相关系数时对变量的分布没有假定
C. Spearman相关系数绝对值越接近于1,相关程度越高。
D. 使用Spearman相关系数时假定变量分布遵循正态分布
第7题:
下列关于相关性对风险影响的说法中,错误的是( )。
A.证券报酬率的相关系数越小,风险分散化效应就越强
B.机会集曲线是否有向左弯曲部分,取决于相关系数的大小
C.机会集是一条直线,表示两种组合的证券相关系数为0
D.机会集曲线越弯曲,证券报酬率的相关系数就越小
第8题:
下列说法不正确的是( )。
A.相关系数为1时,不能分散任何风险
B.相关系数在0~1之间时,相关程度越低风险分散效果越大
C.相关系数在-1~0之间时,相关程度越低风险分散效果越大
D.相关系数为-1时,可以分散所有风险
第9题:
第10题: