 (i=1,2,…,θ,X1,X2,…,Xn为来自总体的简单随机样本,则θ的矩估计量为_______(其中θ为正整数).
(i=1,2,…,θ,X1,X2,…,Xn为来自总体的简单随机样本,则θ的矩估计量为_______(其中θ为正整数).第1题:

第2题:


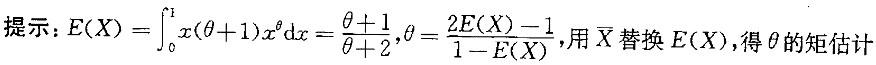

第3题:
设(X1,X2,…,Xn)是来自正态总体N(μ,σ2)的简单随机样本,其中参数μ,σ2未知,则下列各项中,不是统计量的有( )。

第4题:
 P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.第5题:
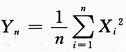 ,依概率收敛于_______.
,依概率收敛于_______.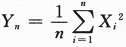 ,依概率收敛于
,依概率收敛于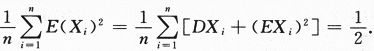 答案应填
答案应填
第6题:

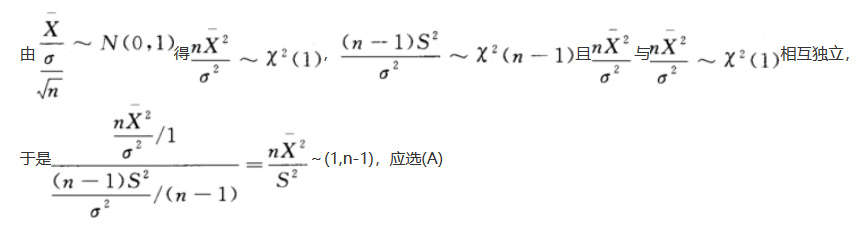
第7题:
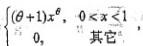 其中θ>-1是未知参数,X1,X2,...Xn是来自总体X的样本,则θ的矩估计量是:
其中θ>-1是未知参数,X1,X2,...Xn是来自总体X的样本,则θ的矩估计量是:

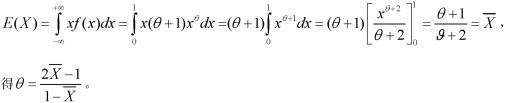
第8题:
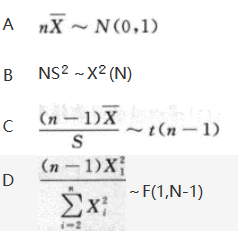
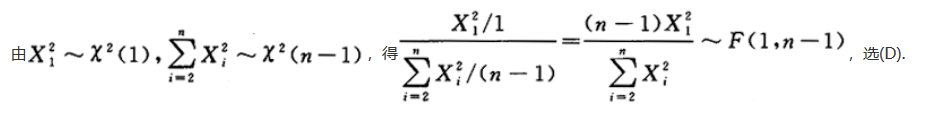
第9题:
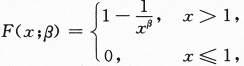

第10题:
 服从_______分布,参数为________.
服从_______分布,参数为________.
