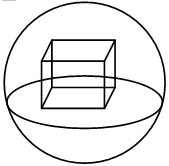
 ,正方体位于半径为3的球内,且其中一面位于球的大圆上,则正方体表面积最大为
,正方体位于半径为3的球内,且其中一面位于球的大圆上,则正方体表面积最大为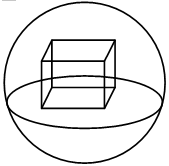
第1题:
把棱长为4的正方体分割成24个棱长为整数的正方体(且没有剩余),其中棱长为1的正方体的个数为( )
A、 12
B、 15
C、 18
D、 21

第2题:
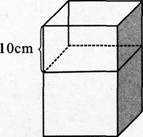
第3题:
把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积总和最小,则小正方体的表面积总和为( )。
A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2
第4题:
第5题:
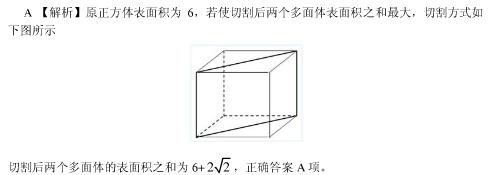
第6题:
第7题:
第8题:
把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积总和最小,则小正方体的表面积总和为( )。
A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2
第9题:
第10题:
