(1)角平分线上的点到角两边的距离相等。 (2)新课导入:
教师:我们应该在很早之前就接触过角的平分线这个概念,谁能告诉我什么是角的平分线呢
(学生回答)一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
教师:大家观察一下这个角,其实,再添加一些线段就能成为两个三角形,我们之前学习了全等三角形的性质及判定,那么结合这个,我们是否能够发现角的平分线的一些性质呢今天我们就来探究一 下这个问题。
设计意图:复习角平分线的定义,并为角平分线的性质定理的引出做铺垫,为下一步设置问题通过折纸及作图过程,由学生自己去发现结论。
教学活动:任意作-一个角∠AOB, 作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA和OB的垂线, 分别记垂足为D, E,PD和PE有什么关系引导学生猜想。
教师:大家可以用直尺来量测一下,能够得到结论吗
大部分同学都得到了PD=PE的结论。 那么有谁能够利用数学方法来证明一下呢
已知:如图,∠AOC=∠BOC, 点P在0C上,PD⊥OA,PE⊥OB,垂足分别为D,E。
求证: PD=PE。
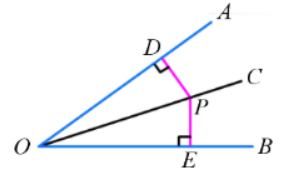
师生共同证明:
∵PD⊥OA,PE⊥OB
∴∠PDO=∠PEO=90°
在ΔPDO和ΔPEO中
∠PDO=∠PEO (已证)
∠AOC=∠BOC
OP=OP (公共边)
∴ΔPDO≌ΔPEO (AAS)
∴PD=PE (全等三角形的对应边相等)
得到角平分线性质:角的平分线上的点到角的两边的距离相等。
教师:通过刚刚的证明,我们得到了我们的结论是正确的。是不是在角平分线上任意取点,都可以得到这个结论呢
(学生动手验证)
教师:我们发现,任意一点都可以得到相等的结论。由此,我们得到了角平分线的性质:
角平分线上的点到角的两边的距离相等。
结论数学语言:
∵OP平分∠AOB,PD⊥OA,PE⊥OB
∴PD=PE。
教师:在这个定理中,我们必须明白,这个性质的应用必须满足几个条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
设计意图:让学生通过实验发现、分析概括、推理证明角的平分线的性质,体会研究几何问题的基本思路,以角的平分线的性质的证明为例,让学生概括几何名命题的-般步骤,发展学生的归纳概括能力。
(3)数学活动经验是一种 属于学生自己的“主观性认识”,对于认识几何图形的数学活动经验,是学生经过数学学习后对整个数学活动过程产生的认识。如何帮助学生积累认识几何图形的数学活动经验,首先要联系直观图形,把生活经验转化为基本数学活动经验。学生在生活中已经积累的一些关于数学的原始、初步的经验,因此要善于捕捉生活中的数学现象,挖掘数学知识的生活内涵,让学生亲身经历将生活经验转化为数学活动经验的过程。例如在本节课中,可以先让学生画一个角,然后探究角平分线的作法。利用模型教具说明平分角的仪器的工作原理,从中受到启发,利用尺规做角的平分线,进-步思考角的平分线上的点的特征。
其次要引导观察、思考推理,丰富学生思维的经验。 积累活动经验总得依赖一些活动,但是所谓的活动并不-定是指直观的操作活动,行为操作的经验是基本活动经验,抽象的思考、探究的经验也是基本活动经验的重要组成部分。例如在本节课中,教师在抛出“PD和PE有什么关系之后,教师先引导学生进行猜想,再带领学生进行自主探究去证明,对于不同的学生想出证明方法可能都不一样,所以教师可以组织学生进行汇报交流,最后师生共同总结得到证明方法:最終得到角平分线定理的性质。


