多元线性回归分析中的 ESS反映了()
第1题:
在一元线性回归模型中,e表示()。
A、估计值Y在回归直线上的截距
B、回归直线的斜率
C、误差即实际值和估计值之间的差额
D、因变量
第2题:
第3题:
根据资料计算的判定系数R2=0.96978,这表明( )。
A.在Y的总变差中,有96.98%可以由解释变量X做出解释
B.回归方程对样本观测值的拟合程度良好
C.在Y的总变差中,有3.02%可以由解释变量X做出解释
D.回归方程对样本观测值的拟合优度不高
第4题:
第5题:
第6题:
下列关于回归平方和的说法,正确的有( )。
A.自变量的变动对因变量的影响引起的变差
B.无法用回归直线解释的离差平方和
C.回归值 与均值
与均值 离差的平方和
离差的平方和
D.实际值y与均值 离差的平方和
离差的平方和
E.总的变差平方和与残差平方和之差
总的变差平方和(SST)可以分解为回归平方和(SSR)和残差平方和(SSE)两部分。其中,∑( )是回归值
)是回归值 与均值
与均值 的离差平方和,它可以看作是y的总变差中由于x与y的线性关系引起的y的变化的那部分,可以由回归直线来解释,因而称为可解释的变差平方和或回归平方和,记为SSR。三个平方和的关系是SST=SSR+SSE。
的离差平方和,它可以看作是y的总变差中由于x与y的线性关系引起的y的变化的那部分,可以由回归直线来解释,因而称为可解释的变差平方和或回归平方和,记为SSR。三个平方和的关系是SST=SSR+SSE。
第7题:
第8题:
下列关于一元线性回归方程说法正确的是( )。
A.是描述两个变量之间相关关系的最简单的回归模型
B.x为因变量,Y为自变量
C.可以用最小二乘法求得一元线性回归方程中的未知常数
D.回归系数表示自变量每变动一个单位时,因变量的平均变化量
E.根据给定自变量的值可以估计因变量的估计值
第9题:
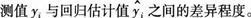
第10题: