假设某班期末统计学考试成绩服从正态分布，平均成绩为70分，标准差为12分，要求计算： （1）随机抽取1人，该同学成绩在82分以上的概率； （2）随机抽取9人，其平均成绩在82分以上的概率。
第1题：
某班统计数学期末考试成绩,平均成绩是84.1分。后来发现小华的成绩是96分,被错记为69分,重新计算后平均成绩为84.7分,那么这个班有()名学生
A.41
B.43
C.45
D.47
第2题：
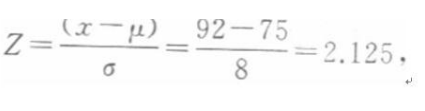
第3题：
A.平均数不变，标准差不变
B.平均数和标准差都增加10分
C.平均数增加10分，标准差不变
D.平均数不变，标准差增加10分
第4题：
第5题：
第6题：
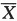，样本标准差记为S.本题就是要在显著性水平α=0.05下检验假设H0：μ=70；H1：μ≠70.
现在μ0=70，n=36.
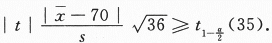
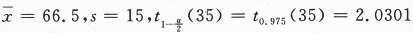，算得
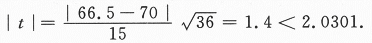
第7题：
第8题：
甲、乙两个班参加同一学科考试，甲班的平均考试成绩为86分，标准差为12分。乙班考试成绩的分布如下：
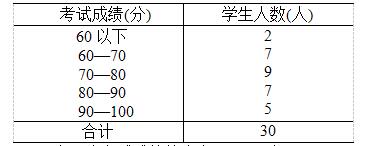
（1）画出乙班考试成绩的直方图。
（2）计算乙班考试成绩的平均数及标准差。
（3）比较甲乙两个班哪个班考试成绩的离散程度大?
参考答案：
第9题：
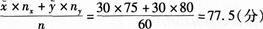
第10题：