下列关于行棋的说法正确的是（）
第1题：
论述题2：以下是某“象棋中走马事件”应用程序的走马规则，请按要求回答问题
以下是中国象棋中走马事件中的走马原则：
1)如果落点在棋盘外，则不移动棋子。
2)如果落点与起点不构成日字型，则不移动棋子。
3)如果落点处有己方棋子，则不移动棋子。
4)如果在落点方向的邻近交叉点有棋子(绊马腿)，则不移动棋子。
5)如果不属于(1)～(4)条，且落点处无棋子，则移动棋子。
6)如果不属于(1)～(4)条，且落点处为对方棋子(非老将)，则移动棋子并除去对方棋子。
7)如果不属于(1)～(4)条，且落点处为对方老将，则移动棋子，并提示战胜对方，
游戏结束。
(1)画出该应用程序的因果图。
(2对该软件进行基于因果图的方法设计测试用例。
问题2：
解答：
根据上面的因果图建立对应的判定表。
在该应用程序中原因有7个一个完整的判定表应有27(上标)=128种情况。由于篇幅的限制且考虑到5、 6、7原因只与中间结果11有关所以这里将完整的判定表拆分为两个子表如表17-12和表17-13所示。对于结果22、23、24中间结果是原因因此在表17-13中将11作为原因。
由表17-12可知当结点11为1时结果21为0。由于结果21、22、23、24受到O约束的限制不能同时为0所以在表17-13中的的2列是不能出现的情况；同样受到O约束的还有8、12、14和16列；由于E约束第7、8、11到16列也是不可能出现的情况。在表中用灰框表示。
最后根据判定表设计测试用例。如表17-13所示判定表中没有被划去的每一列就是一个测试用例。
问题2：
解答：
根据上面的因果图，建立对应的判定表。
在该应用程序中，原因有7个，一个完整的判定表应有27(上标)=128种情况。由于篇幅的限制，且考虑到5、 6、7原因只与中间结果11有关，所以这里将完整的判定表拆分为两个子表，如表17-12和表17-13所示。对于结果22、23、24，中间结果是原因，因此在表17-13中，将11作为原因。
由表17-12可知，当结点11为1时，结果21为0。由于结果21、22、23、24受到O约束的限制，不能同时为0，所以在表17-13中的的2列是不能出现的情况；同样受到O约束的还有8、12、14和16列；由于E约束，第7、8、11到16列也是不可能出现的情况。在表中用灰框表示。
最后根据判定表设计测试用例。如表17-13所示，判定表中没有被划去的每一列就是一个测试用例。 解析：首先分析走马规则，找出所有的原因以及所有可能的结果，结合题目中找出二者的联系，按照因果图的画法规则，画出因果图。然后按照基于因果图的方法设计测试用例。
第2题：
今有甲、乙、丙三堆棋子共98枚。先从甲堆中分棋子给另外两堆，使两堆数各增加一倍，再把乙堆棋子照这样分配一次，最后把丙堆棋子也这样分配，结果甲堆棋子数是丙堆棋数的4/5，乙堆棋子数是丙堆棋子数的22/15。求三堆中原来最多一堆的棋子是多少？（ ）
A．16
B．30
C．52
D．64
第3题：
A、把棋子“组块”成有意义的模式
B、预想的棋着数几乎相同
C、思考的棋着数几乎相同
D、对棋着的搜索模式相似
E、重构棋局的用时更短
第4题：
第5题：
第6题：
阅读下列说明，回答问题1至问题3。
【说明】
因果图方法的思路是：从用自然语言书写的程序规格说明描述中找出因(输入条件)和果(输出或程序状态的改变)，通过因果图转换为判定表。
分析中国象棋中走马的实际情况(下面未注明的均指的是对马的说明)，马走日字型(邻近交叉点无棋子)，遇到对方棋子可以吃掉，遇到本方棋子不能落到该位置。
应用中可能有多种输入条件，在什么情况下可采用因果图法设计测试用例?
根据上述说明，利用因果图法，下面列出走棋出现的情况和结果，找出哪些是正确的输入条件，哪些是正确的输出结果，请把相应的字母编号填入表中。 A．落点在棋盘上； B．落点与起点构成日字；
C．移动棋子； D．落点处为对方棋子：
E．落点处为自己方棋子；F．移动棋子，并除去对方棋子；G．落点方向的邻近交叉点无棋子；H．不移动棋子；I．落点处无棋子。
下图画出中国象棋中走马的因果图，请把问题2中列出的输入条件和输出结果的字母编号填入到空白框中相应的位置。
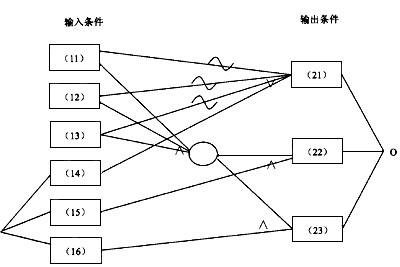
请帮忙给出每个问题的正确答案和分析，谢谢！
第7题：
丁丁和宁宁各有一只盒子，里面都放着棋子，两只盒子里的棋子一共是270粒。丁丁从自己的盒子里拿出÷的棋子放入宁宁的盒子里后，宁宁盒子里的棋子数恰好增加亡。原来宁宁有棋子多少粒?（ ）
A．180
B．150
C．120
D．145
第8题：
在九宫格棋盘上，两位选手轮流在棋盘上摆各自的棋子(每次一枚)，谁先取得三子一线的结果就取胜。设程序方MAX的棋子用(×)表示，对手MIN的棋子用(○)表示，MAX先走。静态估计函数f(p)规定如下：若p对任何一方来说都不是获胜的格局，则f(p)=(所有空格都放上MAX的棋子之后，MAX的三子成线(行、列、对角)的总-(所有空格都放上MIN的棋子之后，MIN的三子成线(行、列、对角)的总数)。当×在中央位置，○在中上位置时，则可得f(p)=_。
A、1
B、2
C、4
D、6
第9题：
第10题：