违法和不良信息举报 联系客服
免费注册 登录

设K是个数域，K[x]中的多项式f（x），g（x），若有f=g，则可以得到什么？（）

题目
单选题
设K是个数域，K[x]中的多项式f（x），g（x），若有f=g，则可以得到什么？（）
A

f（x）=g（f（x））

B

g（x）=f（f（x））

C

f（x）=g（x）

D

g（x）=f（g（x））

参考答案和解析
正确答案： C
解析： 暂无解析
如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

函数f(x)=2x＋3,g(x)=6x＋k,且f[g(x)]=g[f(x)]则k=()

A、0

B、15

C、10

D、不存在


参考答案：B

第2题：

设f(x)，g(x)ϵP[x J. 若f(x)lg(x)，g(x)lf(x)，则 f(x)与g(x)的关系是( ).


参考答案：A

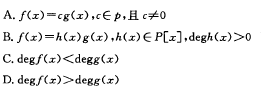
第3题：

设f(x)=3x,g(x)=x2，则函数g[f(x)]-f[g(x)]=_______________.


正确答案：

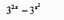
第4题：

设函数f（x），g（x）是大于零的可导函数，且f′（x）g（x）-f（x）g′（x）＜0，则当a＜x＜b时有（ ）《》（ ）

A.f（x）g（b）＞f（b）g（x）
B.f（x）g（a）＞f（a）g（x）
C.f（x）g（x）＞f（b）g（b）
D.f（x）g（x）＞f（a）g（a）

答案：A
解析：

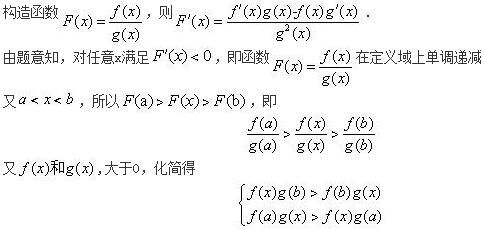
第5题：

设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（　　）。

A． [f（x）/g（x）]＞[f（a）/g（b）]
B． [f（x）/g（x）]＞[f（b）/g（b）]
C． f（x）g（x）＞f（a）g（a）
D． f（x）g（x）＞f（b）g（b）

答案：C
解析：
因为[f（x）g（x）]′＝f′（x）g（x）＋f（x）g′（x）＞0，所以函数f（x）g（x）在[a，b]上单调递增。所以，当x∈（a，b）时，f（a）g（a）＜f（x）g（x）＜f（b）g（b）。

第6题：

设f (x)=x2,g(x)=ex,则f [g(x)]=_________.


正确答案：
e2x

第7题：

设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（　　）。

A． f[g（x）]
B． f[f（x）]
C． g[f（x）]
D． g[g（x）]

答案：D
解析：
D项，令T（x）＝g[g（x）]。因为T（－x）＝g[g（－x）]＝g[－g（x）]＝－g[g（x）]，所以T（－x）＝－T（x），所以g[g（x）]为奇函数。

第8题：

设f(x),g(x),h(x)均为奇函数,则()中所给定的函数是偶函数。

A、f(x)g(x)h(x)

B、[f(x)+g(x)]h(x)

C、f(x)+g(x)

D、f(x)+g(x)+h(x)


参考答案：B

第9题：

设函数f(x)=x+aln(1+x)+bxsinx，g(x)=kx^3，若f(x)与g(x)在x→0是等价无穷小，求a，b，k值.


答案：
解析：

第10题：

在F（x）中，f（x），g（x）是次数≤n的多项式，若在F中有n+1个不同的元素，c1，c2…使得f（ci）=g（ci），则f（x）=g（x）。


正确答案:正确

更多相关问题
相关内容