临床药物治疗学
药理学
药事法律
药学服务
第1题:
课程计划的构成包括以下几方面:_________的设置、学科顺序、课时分配、学年编制与学周安排。
第2题:
第3题:
在在SQL Server 2000中,设有课程表(课程号,课程名,学分,开课学期),现要在此关系表上建立一个查询指定学期开设的课程总门数和总学分数的内嵌表值函数,函数名为f _FindTotal。实现这个函数的正确代码是
A.CREATE FUNCTION f_FindTotal(@semester int) RETURNS table AS RETURN( SELECT COUNT(课程号)as课程门数, SUM(学分)as总学分FROM课程表 WHERE开课学期 = @ semester)
B.CREATE FUNCTION f_FindTotal(@semester int) RETURNS table AS RETURN( SELECT COUNT(课程号)as课程门数, COUNT(学分)as总学分FROM课程表 WHERE开课学期 = @semester)
C.CREATE FUNCTION f_FindTotal(@semester int) RETURNS table AS RETURN( SELECT SUM(课程号)as课程门数, SUM(学分)as总学分FROM课程表 WHERE开课学期= @semester)
D.CREATE FUNCTION f_FindTotal(@semester int) RETURNS table AS RETURN( SELECT SUM(课程号)as课程门数, COUNT(学分)as 总学分FROM课程表 WHERE开课学期 = @semester)
第4题:
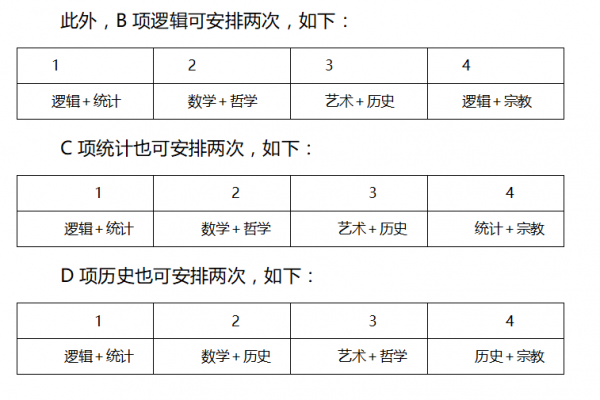
第5题:
第6题:
某学院10名博士生(B1~B10)选修6门课程(A~F)的情况如下表(用√表示选修)所示。
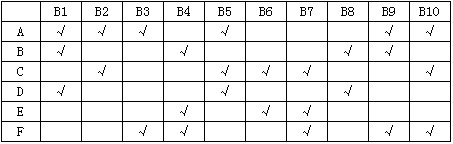
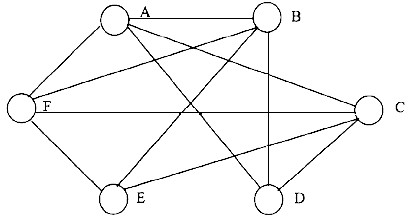
现需要安排这6门课程的考试,要求是:(1) 每天上、下午各安排一门课程考试,计划连续3天考完;(2) 每个博士生每天只能参加一门课程考试,在这3天内考完全部选修课;(3) 在遵循上述两条的基础上,各课程的考试时间应尽量按字母升序做先后顺序安排(字母升序意味着课程难度逐步增加)。 为此,各门课程考试的安排顺序应是(56)。
A.AE,BD,CF
B.AC,BF,DE
C.AF,BC,DE
D.AE,BC,DF

第7题:
第8题:
综合实践活动课程要求的课时安排应是弹性课时制,即将每周4课时的综合实践活动时间根据需要灵活安排。( )
第9题:

第10题:
博士学位是美国高等学校授予的最高学位,包括()。
A职业博士
B专业博士
C研究博士
D应用博士
E理论博士