奇函数
偶函数
周期函数
单调函数
第1题:
设f(x)为连续函数,F(x)是f(x)的原函数,则( )。
(A) 当f(x)是奇函数时,F(x)必为偶函数
(B) 当f(x)是偶函数时,F(x)必为奇函数
(C) 当f(x)是周期函数时,F(x)必为周期函数
(D) 当f(x)是单增函数时,F(x)必为单增函数
(E) 当f(x)是单减函数时,F(x)必为单减函数
第2题:
(3)命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
(A)若f(x) 是偶函数,则f(-x)是偶函数
(B)若f(x)不是奇函数,则f(-x)不是奇函数
(C)若f(-x)是奇函数,则f(x)是奇函数
(D)若f(-x)不是奇函数,则f(x)不是奇函数
第3题:
A、偶函数
B、奇函数
C、非奇非偶函数
D、可能是奇函数也可能是偶函数
第4题:
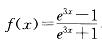 ,则:
,则:

第5题:

第6题:
【题目描述】
1.设f(x)为连续函数,F(x)是f(x)的原函数,则( )。
(A) 当f(x)是奇函数时,F(x)必为偶函数
(B) 当f(x)是偶函数时,F(x)必为奇函数
(C) 当f(x)是周期函数时,F(x)必为周期函数
(D) 当f(x)是单增函数时,F(x)必为单增函数
(E) 当f(x)是单减函数时,F(x)必为单减函数
正确答案:A
第7题:
第8题:
A、偶函数
B、奇函数
C、非奇非偶函数
D、F(x)≡0
第9题:
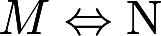 表示“M的充分必要条件是N”,则必有
表示“M的充分必要条件是N”,则必有
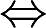 f(x)是奇函数
f(x)是奇函数
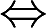 f(x)是偶函数
f(x)是偶函数
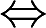 f(x)是周期函数
f(x)是周期函数
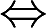 f(x)是单调函数
f(x)是单调函数
第10题: