对
错
第1题:
第2题:
当向一棵m阶的B—树做插入操作时,若一个结点中的关键字个数等于______,则必须分裂为2个结点。
A.m
B.m-1
C.m+l
D.[m/2]
第3题:
下面关于B树运算的叙述中,正确的是
A.若插入过程中根结点发生分裂,则B树的高度加1
B.每当进行插入运算,就往B树的最下面一层增加一个新结点
C.若要删除的关键码出现在根结点中,则不能真正删除,只能做标记
D.删除可能引起B树结点个数减少,但不会造成B树高度减小
第4题:
阅读以下说明和C代码,填补代码中的空缺,将解答填入答题纸的对应栏内。 【说明】 二叉查找树又称为二叉排序树,它或者是一棵空树,或者是具有如下性质的二叉树。 (1)若它的左子树非空,则左子树上所有结点的值均小于根结点的值。 (2)若它的右子树非空,则右子树上所有结点的值均大于根结点的值。 (3)左、右子树本身就是两棵二叉查找树。 二叉查找树是通过依次输入数据元素并把它们插入到二叉树的适当位置上构造起来的,具体的过程是:每读入一个元素,建立一个新结点,若二叉查找树非空,则将新结点的值与根结点的值相比较,如果小于根结点的值,则插入到左子树中,否则插入到右子树中;若二叉查找树为空,则新结点作为二叉查找树的根结点。 根据关键码序列{46,25,54,13,29,91}构造一个二叉查找树的过程如图4-1所示。 设二叉查找树采用二叉链表存储,结点类型定义如下: typedef int KeyType; typedef struct BSTNode{ KeyType key; struct BSTNode *left,*right; }BSTNode,*BSTree; 图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。
设二叉查找树采用二叉链表存储,结点类型定义如下: typedef int KeyType; typedef struct BSTNode{ KeyType key; struct BSTNode *left,*right; }BSTNode,*BSTree; 图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。 图4-2 函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中,若插入成功,函数返回1,否则返回0。
图4-2 函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中,若插入成功,函数返回1,否则返回0。
【C代码】 int lnsertBST(BSTree*rootptr,KeyType kword) /*在二叉查找树中插入一个键值为kword的结点,若插入成功返回1,否则返回0; *rootptr为二叉查找树根结点的指针 */ { BSTree p,father; (1) ; /*将father初始化为空指针*/ p=*rootptr; /*p指示二叉查找树的根节点*/ while(p&& (2) ){ /*在二叉查找树中查找键值kword的结点*/ father=p; if(kword<p->key) p=p->left; else p=p->right; } if( (3) )return 0; /*二叉查找树中已包含键值kword,插入失败*/ p=(BSTree)malloc( (4) ); /*创建新结点用来保存键值kword*/ If(!p)return 0; /*创建新结点失败*/ p->key=kword; p->left=NULL; p->right=NULL; If(!father) (5) =p; /*二叉查找树为空树时新结点作为树根插入*/ else if(kword<father->key) (6) ; /*作为左孩子结点插入*/ else (7) ; /*作右孩子结点插入*/ return 1; }/*InsertBST*/
第5题:
以下关于B树运算的叙述中,哪一条是正确的?
A.若插入过程中根节点发生分裂,则B树的高度加1
B.每当进行插入运算,就在B树的最下面一层增加一个新节点
C.若要删除的关键码出现在根节点中,则不能真正删除,只能做标记
D.删除可能引起B树节点个数减少,但不会造成B树高度减少
第6题:
以下关于B树运算的叙述中,哪一条是正确的?
A.若插入过程中根结点发生分裂,则B树的高度加1
B.每当进行插入运算,就在B树的最下面一层增加一个新结点
C.若要删除的关键码出现在根结点中,则不能真正删除,只能做标记
D.删除可能引起B树结点个数减少,但不会造成B树高度减少
第7题:
当向一棵m阶的B-树做插入操作时,若一个结点中的关键字个数等于______,则必须分裂为2个结点。
A.m
B.m-1
C.m+1
D.m/2
第8题:
以下关于B树运算的叙述中,哪一条是正确的?
A.若插入过程中根结点发生分裂,则B树的高度加1
B.每当进行插入运算,就在B树的最下面一层增加一个新结点
C.若要删除的关键码出现在根结点中,则不能真正删除,只能做标记
D.删除可能引起B树结点个数减少,但不会造成B树高度减小
第9题:
阅读下列说明、图和C代码。
[说明5-1]
B树是一种多叉平衡查找树。一棵m阶的B树,或为空树,或为满足下列特性的m叉树:
①树中每个结点最多有m棵子树;
②若根结点不是叶子结点,则它至少有两棵子树;
⑧除根之外的所有非叶子结点至少有[m/2]棵子树;
④所有的非叶子结点中包含下列数据信息:
(n,A0,K1,A1,K2,A2, …,Kn,An)其中:Ki(i=1,2,…,n)为关键字,且Ki<Ki+1(i=1,2,…,n-1);Ai(i=0,1,…,n)为指向子树根结点的指针,且指针Ai-1,所指子树中所有结点的关键字均小于Ki,Ai+1,所指子树中所有结点的关键字均大于Ki,n为结点中关键字的数目。
⑤所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
例如,一棵4阶B树如下图所示(结点中关键字的数目省略)。
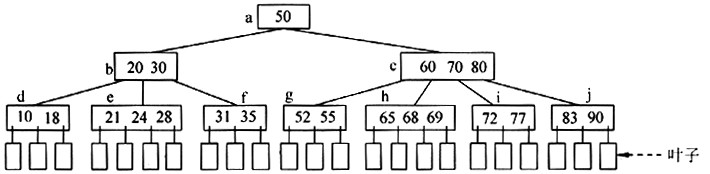
B树的阶M、bool类型、关键字类型及B树结点的定义如下:
define M 4 /*B树的阶*/
typedef enum {FALSE=0,TRUE=1}bool;
typedef int ElemKeyType;
typedef struct BTreeNode {
int numkeys; /*结点中关键字的数日*/
struct BTreeNode*parent; /*指向父结点的指针,树根的父结点指针为空*/
struct BTreeNode *A[M]; /*指向子树结点的指针数组*/
ElemKeyType K[M]; /*存储关键字的数组,K[0]闲置不用*/
}BTreeNode;
函数SearchBtree(BTreeNode*root,ElemKcyTypeakey,BTreeNode:*pb)的功能是:在给定的一棵M阶B树中查找关键字akey所在结点,若找到则返回TRUE,否则返回 FALSE。其中,root是指向该M阶B树根结点的指针,参数ptr返回akey所在结点的指针,若akey不在该B树中,则ptr返回查找失败时空指针所在结点的指针。例如,在上图所示的4阶B树中查找关键字25时,ptr返回指向结点e的指针。
注;在结点中查找关键字akey时采用二分法。
[函数5-1]
bool SearchBtree(BTreeNode* root, ElemKeyType akey, BTreeNode **ptr)
{
int lw, hi, mid;
BTreeNode*p = root;
*ptr = NULL;
while ( p ) {
1w = 1; hi=(1);
while (1w <= hi) {
mid = (1w + hi)/2;
if (p -> K[mid] == akey) {
*ptr = p;
return TRUE;
}
else
if ((2))
hi=mid - 1;
else
1w = mid + 1;
}
*ptr = p;
p = (3);
}
return FALSE;
}
[说明5-2]
在M阶B树中插入一个关键字时,首先在最接近外部结点的某个非叶子结点中增加一个关键字,若该结点中关键字的个数不超过M-1,则完成插入;否则,要进行结点的“分裂”处理。所谓“分裂”,就是把结点中处于中间位置上的关键字取出来并插入其父结点中,然后以该关键字为分界线,把原结点分成两个结点。“分裂”过程可能会一直持续到树根,若树根结点也需要分裂,则整棵树的高度增加1。
例如,在上图所示的B树中插入关键字25时,需将其插入结点e中。由于e中已经有3个关键字,因此将关键字24插入结点e的父结点b,并以24为分界线将结点e分裂为e1和e2两个结点,结果如下图所示。
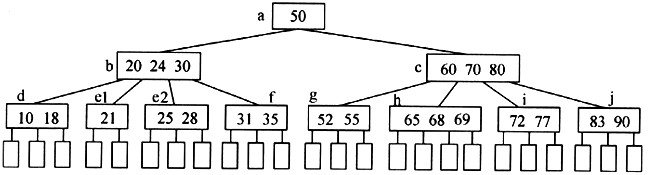
函数Isgrowing(BTreeNode*root,ElemKeyTypeakey)的功能是:判断在给定的M阶B树中插入关键字akey后,该B树的高度是否增加,若增加则返回TRUE,否则返回FALSE。其中,root是指向该M阶B树根结点的指针。
在函数Isgrwing中,首先调用函数SearchBtree(即函数5-1)查找关键字akey是否在给定的M阶B树中,若在,则返回FALSE(表明无需插入关键字akey,树的高度不会增加);否则,通过判断结点中关键字的数目考查插入关键字akey后该B树的高度是否增加。
[函数5-2]
bool Isgrowing(BTreeNode* root, ElernKeyType akey)
{ BTreeNode *t, *f;
if( !SearchBtree((4) )
第10题:
下面关于B树运算的叙述中,正确的是
A.若插入过程甲根结点发生分裂,则B树的高度加1
B.每当进行插入运算,就往B树的最下面一层增加一个新结点
C.若要删除的关键码出现在根结点中,则不能真正删除,只能做标记
D.删除可能引起B树结点个数减少,但不会造成B树高度减小