第1题:
阅读以下说明和流程图,回答问题1~2,将解答填入对应的解答栏内。
[说明]
下面的流程图描述了计算自然数1到N(N≥1)之和的过程。
[流程图]
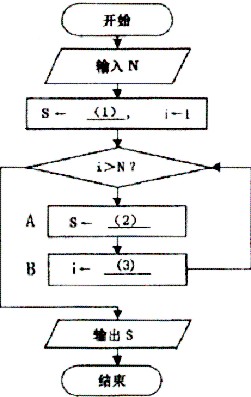
[问题1] 将流程图中的(1)~(3)处补充完整。
[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值,A框内应填写(4);为使流程图能计算并输出不大于N的全体奇数之和,B框内应填写(5)。
第2题:
阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。
【说明】
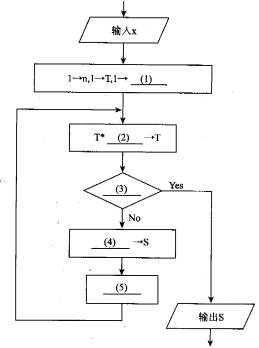
下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。
【流程图】
第3题:
函数fib1、fib2求得菲波那契数列第n项(n>40)的速度并不相同,清指出速度慢的函数名,并简要说明原因。
第4题:
阅读以下说明和流程图,回答问题将解答填入对应栏内。
[说明]
已知递推数列:a(1)=1,a (2s)= a (s),a(2s+1)=a (s)+a (s+1)(s 为正整数)。试求该数列的第n项与前n项中哪些项最大?最大值为多少?
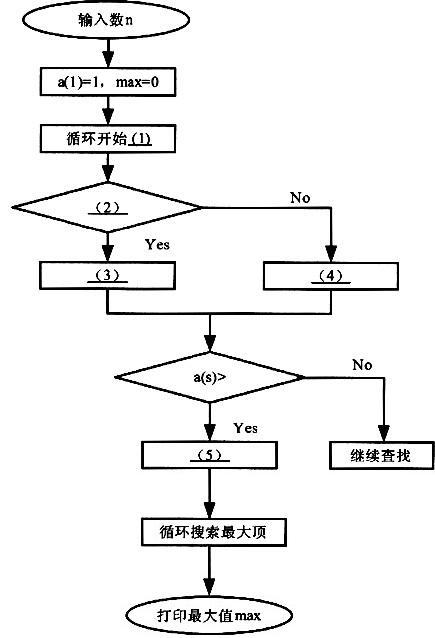
算法分析:该数列序号分为奇数或偶数两种情况做不同递推,所得数列呈大小有规律的摆动。设置a数组,赋初值a (1)=1。根据递推式,在循环中分项序号s (2~n)为奇数或偶数作不同递推:每得一项 a (s),即与最大值max 作比较,如果a (s)>max,则max=a(i)。最后,在所有项中搜索最大项(因最大项可能多于一项),并打印最大值max。
[问题]
将流程图中的(1)~(5)处补充完整。
注:流程图中(1)循环开始的说明按照“循环变量名:循环初值,循环终值,增量”格式描述。
[流程图]
第5题:
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。
【说明】
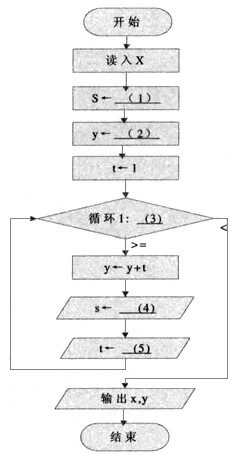
下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值,其中用ε(>0)表示误差要求。
【流程图】
第6题:
阅读下列说明和流程图,将应填入(n)的字句写在对应栏内。
【说明】
下列流程图(如图4所示)用泰勒(Taylor)展开式
sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x2n+1/(2n+1)!+…
【流程图】
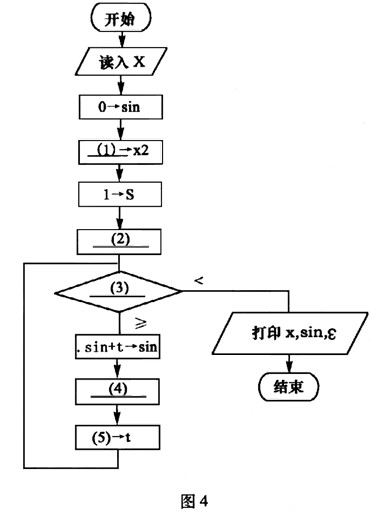
计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
第7题:
阅读以下说明和C函数代码,回答问题并将解答写在对应栏内。
【说明】
著名的菲波那契数列定义式为
f1=1 f2=1 fn=fn-1+fn-2 (n=3,4,…)
因此,从第1项开始的该数列为1,1,2,3,5,8,13,21,…。函数fibl和fib2分别用递归方式和迭代方式求解菲波那契数列的第n项(调用fib1、fib2时可确保参数n获得一个正整数)。
【C函数代码】

函数fib1和fib2存在错误,只需分别修改其中的一行代码即可改正错误。
(1)函数fib1不能通过编译,请写出fib1中错误所在行修改正确后的完整代码。
(2)函数fib2在n≤2时不能获得正确结果,请写出fib2中错误所在行修改正确后的完整代码。
第8题:
下面的程序是求菲波那契(Fibonacci)数列的前10项。已知该数列的前两项都为1,即F(1)=1,F(2)=1;而后面各项满足: F(n)=F(n-1)+F(n-2)。请在程序的每条横线处填写一条语句,使程序的功能完整。
注意:请勿改动main()主方法和其他已有的语句内容,仅在横线处填入适当的语句。
public class Fibonacci{
public static void main(String args[]){
System.out.printtn("Fibonacci is"+" "+"_______________________);
}
static long fib(int n){
if(______________)
return 1;
else
return _________________
}
}
第9题:
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。
【说明】对于大于1的正整数n,(x+1)n可展开为下面流程图的作用是计算(x+1)n展开后的各项系数(i=0,1,....,n)并依次存放在数组A[0...n]中。方法是依次计算k=2,3,..,n时(x+1)k的展开系数并存入数组A,在此过程中,对任一确定的k,利用关系式,按照i递减的顺序逐步计算并将结果存储在数组A中。其中,和都为1,因此可直接设置A[0]、A[k]的值为1。 例如,计算(x+1)3的过程如下:先计算(x+1)2(即k=2)的各项系数,然后计算(x+1)3(即k=3)的各项系数。K=2时,需要计算,和,并存入A[0],A[1]和A[2],其中A[0]和A[1]的值已有,因此将(即A[1])和即(A[0])相加得到的值并存入A[1]。k=3时,需要计算,和和,先计算出(由)得到并存入A[2],再计算(由得到)并存入A[1]。
【流程图】
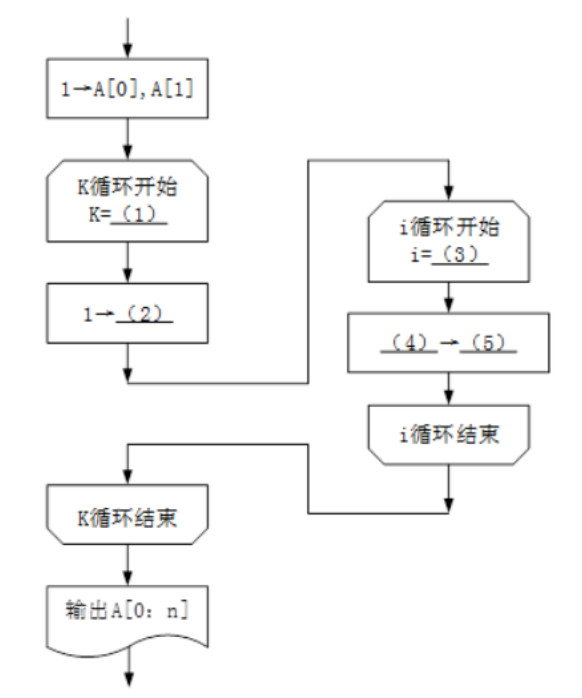
(1)2,n,1
(2)A[k]
(3)k-1,1,-1
(4)A[i]+A[i-1]
(5)A[i]
第10题:
阅读以下说明和流程图,回答问题1-2,将解答填入对应的解答栏内。
[说明]
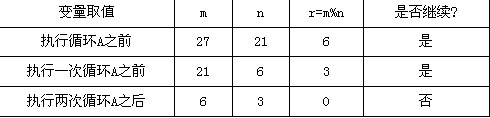
下面的流程图采用欧几里得算法,实现了计算两正整数最大公约数的功能。给定正整数m和 n,假定m大于等于n,算法的主要步骤为:
(1)以n除m并令r为所得的余数;
(2)若r等于0,算法结束;n即为所求;
(3)将n和r分别赋给m和n,返回步骤(1)。
[流程图]
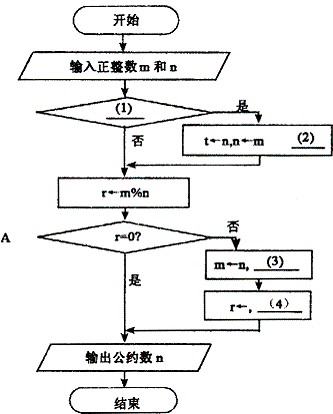
[问题1] 将流程图中的(1)~(4)处补充完整。
[问题2] 若输入的m和n分别为27和21,则A中循环体被执行的次数是(5)。