第1题:
______从二叉树的任一结点出发到根的路径上,所经过的结点序列必按其关键字降序排列。
A.二叉排序树
B.大顶堆
C.小顶堆
D.平衡二叉树
第2题:
高度为h的堆中,最多有(52)个元素,最少有(53)个元素,在大根堆中,关键字最小的元素可能存放在堆的(54)地方。
A.2h-1
B.2h-1
C.2h
D.2h+1
第3题:
此题为判断题(对,错)。
第4题:
中从任一结点出发到根的路径上,所经过的结点序列必按其关键字降序排列。
A.二叉排序树
B.大顶堆
C.小顶堆
D.最优二叉树
第5题:
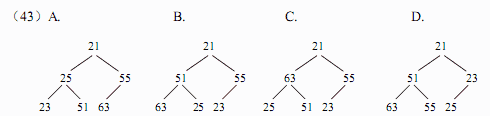
对于n个元素的关键字序列{k1,k2,…,kn},若将其按次序对应到一棵具有n个结点的完全二叉树上,使得任意结点都不大于其孩子结点(若存在孩子结点),则称其为小顶堆。根据以上定义,(43)是小顶堆。
A.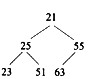
B.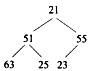
C.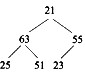
D.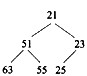
第6题:

第7题:
● 对于n 个元素的关键字序列{k1,k2,…,kn}, 若将其按次序对应到一棵具有 n 个结点的完全二叉树上, 使得任意结点都不大于其孩子结点(若存在孩子结点), 则称其为小顶堆。根据以上定义, (43) 是小顶堆
第8题:
● (45) 从二叉树的任一结点出发到根的路径上,所经过的结点序列必按其关键字降序排列。
(45) A.二叉排序树
B.大顶堆
C.平衡二叉树
D.小顶堆
第9题:
______从二叉树的任一节点出发到根的路径上,所经过的节点序列必须按其关键字降序排列。
A.二叉排序树
B.大顶堆
C.小顶堆
D.平衡二又树
第10题:
试题四(共15分)
阅读下列说明和C代码,回答问题1至问题 3,将解答写在答题纸的对应栏内。
【说明】
堆数据结构定义如下:
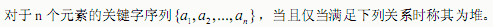
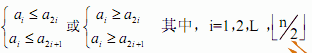
在一个堆中,若堆顶元素为最大元素,则称为大顶堆;若堆顶元素为最小元素,则称为小顶堆。堆常用完全二叉树表示,图4-1 是一个大顶堆的例子。
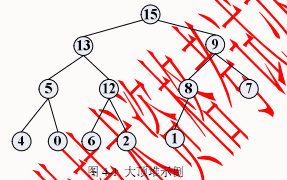
堆数据结构常用于优先队列中,以维护由一组元素构成的集合。对应于两类堆结构,优先队列也有最大优先队列和最小优先队列,其中最大优先队列采用大顶堆,最小优先队列采用小顶堆。以下考虑最大优先队列。
假设现已建好大顶堆A,且已经实现了调整堆的函数heapify(A, n, index)。
下面将C代码中需要完善的三个函数说明如下:
(1)heapMaximum(A):返回大顶堆A中的最大元素。
(2)heapExtractMax(A):去掉并返回大顶堆 A的最大元素,将最后一个元素“提前”到堆顶位置,并将剩余元素调整成大顶堆。
(3)maxHeapInsert(A, key):把元素key插入到大顶堆 A的最后位置,再将 A调整成大顶堆。
优先队列采用顺序存储方式,其存储结构定义如下:
define PARENT(i) i/2
typedef struct array{
int *int_array; //优先队列的存储空间首地址
int array_size; //优先队列的长度
int capacity; //优先队列存储空间的容量
} ARRAY;
【C代码】
(1)函数heapMaximum
int heapMaximum(ARRAY *A){ return (1) ; }
(2)函数heapExtractMax
int heapExtractMax(ARRAY *A){
int max;
max = A->int_array[0];
(2) ;
A->array_size --;
heapify(A,A->array_size,0); //将剩余元素调整成大顶堆
return max;
}
(3)函数maxHeapInsert
int maxHeapInsert(ARRAY *A,int key){
int i,*p;
if (A->array_size == A->capacity) { //存储空间的容量不够时扩充空间
p = (int*)realloc(A->int_array, A->capacity *2 * sizeof(int));
if (!p) return -1;
A->int_array = p;
A->capacity = 2 * A->capacity;
}
A->array_size ++;
i = (3) ;
while (i > 0 && (4) ){
A->int_array[i] = A->int_array[PARENT(i)];
i = PARENT(i);
}
(5) ;
return 0;
}
【问题 1】(10分)
根据以上说明和C代码,填充C代码中的空(1)~(5)。
【问题 2】(3分)
根据以上C代码,函数heapMaximum、heapExtractMax和 maxHeapInsert的时间复杂度的紧致上界分别为 (6) 、 (7) 和 (8) (用O 符号表示)。
【问题 3】(2分)
若将元素10插入到堆A =〈15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1〉中,调用 maxHeapInsert函数进行操作,则新插入的元素在堆A中第 (9) 个位置(从 1 开始)。