第1题:
计算题:设某厂商只把劳动作为可变要素,其生产函数为Q=-0.01L3+L2+36L,Q为厂商每天产量,L为工人的日劳动小时数。所有市场均为完全竞争的,单位产品价格为0.10美元,小时工资率为4.8美元,试求当厂商利润极大时:
(1)厂商每天将投入多少劳动小时?
(2)如果厂商每天支付的固定成本为50美元,厂商每天生产的纯利润为多少?
(1)因为Q=-0.01L3+L2+36L所以MPP=-0.03L2+2L+36
又因为VMP=MPP•P利润最大时W=VMP
所以0.10(-0.03L2+2L+36)=4.8
得L=60
(2)利润=TR-TC=P•Q-(FC+VC)
=0.10(-0.01•603+602+36•60)-(50+4.8•60)
=22
第2题:
已知生产函数Q=f(L,K)=2KL-0.5L2-0.5K2,假定厂商目前处于短期生产,且K=10,
求:
(1)写出在短期生产中该厂商关于劳动的总产量TPL函数、劳动的平均产量APL函数和劳动的边际产量MPL函数。
(2)分别计算当总产量TPL、劳动平均产量APL和劳动边际产量MPL各自达到极大值时的厂商劳动的投入量。(3)什么时候APL=MPL?它的值又是多少?
(1)短期生产中K是不变的,短期关于劳动的总产量函数为:
第3题:
A、PL/PK
B、PK/PL
C、-PL/PK
D、-PK/PL
第4题:
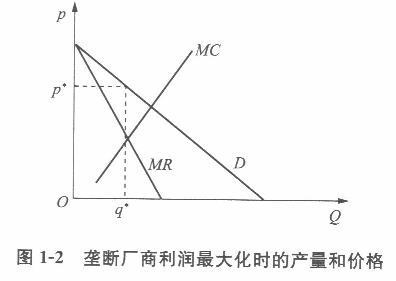
第5题:
假定某厂商的边际成本函数MC=3Q2-30Q+100,且生产10单位产量时的总成本为1000。求:(1)固定成本的值。(2)总成本函数、总可变成本函数,以及平均成本函数、平均可变成本函数。
(1)固定成本为500。

(1)

(2)

第6题:
已知某企业的生产函数Q=L2/3K1/3 ,劳动的价格W=2,资本的价格r=1,
求:
(1)当成本C=3000时,企业实现最大产量时的L、K和Q的值。
(2)当产量Q=800时,企业实现最少成本时的L、K和C的值。
如图:
L=800K=800 C=2L+K=3×800=2400
第7题:
已知生产函数Q=LK,当Q=10时,PL= 4,PK = 1
求(1)厂商最佳生产要素组合时资本和劳动的数量是多少?
(2)最小成本是多少?
第8题:
计算题:假定某厂商只有一种可变要素劳动L,产出一种产品Q,固定成本为既定,短期生产函数Q=-0。1L3+6L2+12L,求:
(1)劳动的平均产量AP为最大值时的劳动人数
(2)劳动的边际产量MP为最大值时的劳动人数
(3)平均可变成本极小值时的产量
(1)因为:生产函数Q=-0.1L3+6L2+12L
所以:平均产量AP=Q/L=-0.1L2+6L+12
对平均产量求导,得:-0.2L+6
令平均产量为零,此时劳动人数为平均产量为最大。L=30
(2)因为:生产函数Q=-0.1L3+6L2+12L
所以:边际产量MP=-0.3L2+12L+12
对边际产量求导,得:-0.6L+12
令边际产量为零,此时劳动人数为边际产量为最大。L=20
(3)因为:平均产量最大时,也就是平均可变成本最小,而平均产量最大时L=30,所以把L=30代入Q=-0。1L3+6L2+12L,平均成本极小值时的产量应为:Q=3060,即平均可变成本最小时的产量为3060。
第9题:
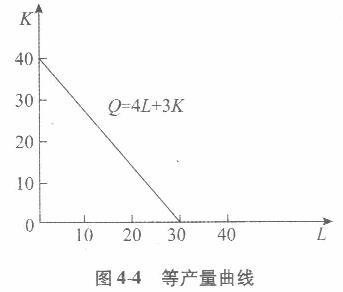

第10题: