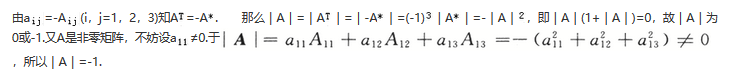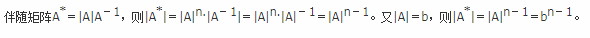A、A=0
B、A=E
C、r(A)=n
D、0r(A)(n)
实数向量空间V={(x1,x2,x3)|x1+x2+x3=0}的维数是_________.
设σ是欧氏空间V的对称变换,则σ在V的标准正交基下的矩阵_______
若已知一个栈的入栈序列是1、2、3、……、n,其输出序列是p1、p2、p3、……、Pn,则pi为
A.i
B.n-i
C.n-i+l
D.不确定
以下程序是一个函数,功能是求二阶矩阵(m行n列矩阵)的所有靠外侧的各元素值之和。(本程序中二阶矩阵用一维数组来表示。)
例如,矩阵为:
3 0 0 3
2 5 7 3
1 0 4 2
则所有靠外侧的各元素值之和为3+0+0+3+2+3+1+0+4+2=18。
add(int m,int n,int arr[])
{ int i,j,sum=0;
for(i=0;i
for(j=0;j<N;J++)
sum=sum+ (7) ;
for(j=0;j
for(i=1; (8) ;i++)
sum=sum+arr[i*n+j];
return(sum);
}
实用文档高等代数(下)期末考试t卷及答案(B卷)一.填空题(每小题3分,共21分).在Px3中,x2-2x-3 在基 1, (x-1), (x-1)2下的坐标为.设n阶矩阵A的全体特征值为储,儿2,111,3,“X)为任一多项式,则f(A)的 全体特征值为.在数域P上的线f*空间Px n中,定义线T*变换A: A( f ( x )=广(x ),则A的值域A Px n =, A的核 A,(0)=1004,已知3阶入-矩阵A (入)的标准形为 0九 0 ,则A (入)的不变 、0 0九2 十九/因子 3阶行歹!j式因子 D3 =.若4阶方阵A的初等因子是(入-1) 2,(入-2),(入-3),则A的若当标准形J=.在n维欧氏空间V中,向量且在标 准正交基,1下的坐 标是(Xi,X2,|,Xn),那么(3i)=.两个有限维欧氏空间同构的充要条件是.选择题(每小题2分,共10分).() 已知V =(a + bi,c + di)a,b,c,dw R为 R上的线性空间,则dim(V)为(A) 1;(B) 2;(C) 3;(D) 4.()下列哪个条件不是n阶复系数矩阵A可对角化的充要条件(A) A有n个线性无关的特征向量;(B) A的初等因子全是1次的;(C) A的不变因子都没有重根;(D) A有n个不同的特征根;.()设三阶方阵A的特征多项式为f (九) = K3 -2九2 -2九+3,则|A尸文案大全实用文档(A) 1;(B) 2;(C) 3;(D) -3.() 设 % =(0,1,1)2=(2,1,2),P =ko(i+ot2,若 P 与。2 正交,贝1(A) k=1;(B) k=4;(C) k= 3;(D) k=2.()下列子集哪个不是R3的子空间33 .一(A)wi- ( xl, x2 ,x3)R| x2 = 1(B)W2= ( Xi, X2, X3 ) - R| X3 =0(C)W3=( X1,X2, x3)R 1X1 = X2 = X3(D)W4= ( X1, X2 ,x3)- R1 X1 = X2 - X3三.判断题(对的打,错的打 X,每小题2分,共12分).()设丫 = Pnn ,则0=A Aw Pn刈,A =0是V的子空间.()鸟,|,%是n维欧氏空间的一组基,矩阵A=(aQ,其中n::nau =(ei, j),则A是正定矩阵.()若n维向量空间Pn含有一个非零向量,则它必含有无穷多个向量.()在线性空间R2中定义变换:o(x,y)=(1 + x,y),则是R的一个 线性变换.()设V是一个欧氏空间,ot, P V ,并且=| P| ,则2+ P与- P正交c.()入一矩阵A(入)可逆的充要条件是|A(K) #0.四.计算题(3小题,共30分).已知值关于基瓦日2f3的坐标为(1,0, 2),由基%,%,%到基九葭久的令2 4”过渡矩阵为10 0,求关于基巴尸?,气的坐标.(8分)e 1 0文案大全实用文档.设V是数域P上一个二维线性空间,环生和1, L是V的两组基,V的线,一 一,广2 1、一一 .、性变换A在基环5下的矩阵为,又从基备,和到基,“2的过渡10;111、.矩阵为|,求A在基7, %下的矩阵.(8分)1-1 2.用正交线性替换X =TY化下列二次型为标准型,并写出相应的正交矩阵T:2 八 2 八 2f(x)=x1 -2x2 -2x3 -4X1X2+4X1X3+8X2X3(14 分)文案大全实用文档五.证明题(每题9分,共27分).设V为数域P上的n维线性空间,叫,”2,11,4为V的一组基,证明V= L( ?1, :-1 - : 2, HL :-1 - : 2 ,口 : n).设。,丁都是数域P上线性空间V的线性变换,且6 = g ,证明Im(。)和Ker (都是t的不变子空间.文案大全实用文档2006高等代数(下)试题解答二 填空题(每小题3分,共21分)1、在 Px3 中,x2 -2x -3在基 1, (x-1), (x-1)2 下的坐标为 (-4, 0, D 。2_,. 2 2x 2x 3 = S (x -1)2、设n阶矩阵A的全体特征值为 九 1,,小川,卜.f(x)为任一多项式,则 f(A)的全体特征值为f( 1),., f( n)一、填空题(每小题3分,共21分)3、在数域P上的线,卜空间Px n中,定义线性变换 TOC o 1-5 h z A:A(f(x)=f (x),则 A 的值域 A(Pxn = Px n.1,A 的核 A+0)=P,彳004、已知3阶入-矩阵A (入)的标准形为0九 0-2 -9 0 九 十ZJ则A (入)的不变因子1,入、入(入+1);3阶行列式因子 d3=- 2(入 +1).二 填空题(每小题3分,共21分)5、若4阶方阵A的初等因子是(入-1)2,(入-2),(入-3),则A的若当标准形J= 1 12I 3 J6、在n维欧氏空间V中,向量占在标准正交基1, 2,川,n下的坐标是(XiIILXn)那么(,i)= Xix xx1 1xi xn n,I =x,1,