最小二乘法的基本原理是:在所有拟合的直线中,与所测实际数据的偏差平方和最大的那条直线为最优
第1题:
当所给数据点的分布并不一定近似地呈一条直线,这时仍用直线拟合显然是不合适的,可用多项式拟合。()
第2题:
此题为判断题(对,错)。
第3题:
用最小二乘法以利润率为因变量拟合直线回归方程,其最小二乘法的原理是使( )。
A.实际Y值与理论 值的离差和最小
B.实际Y值与理论 值的离差平方和最小
C.实际Y值与Y平均值的离差和最小
D.实际Y值与Y平均值的离差平方和最小
第4题:


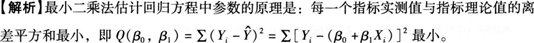
第5题:
用最小二乘法以利润率为因变量拟合直线回归方程,其最小二乘法的原理是使( )。
A.实际Y值与理论Y值的离差和最小
B.实际Y值与理论Y值的离差平方和最小
C.实际Y值与Y平均值的离差和最小
D.实际Y值与Y平均值的离差平方和最小
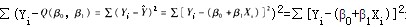 最小。
最小。
第6题:
此题为判断题(对,错)。
第7题:
用最小二乘法拟合回归直线方程,其基本原理是( )。
第8题:
如果所有的观测点都落在回归直线上,R2=1说明()。
A.回归直线不能解释因变量的所有变化
B.因变量的变化与自变量无关
C.回归直线可以解释因变量的所有变化
D.回归直线的拟合效果很好
E.回归直线的拟合效果很差
第9题:

第10题:
最小二乘法的原理是,当所有的测量数据的()最小时,所拟合的直线最优。