一般项的极限为0
一般项n次方根的极限等于1
后项与前项之比的极限小于1
后项与前项之积的极限大于1
第1题：
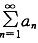收敛是级数
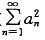收敛的什么条件？
第2题：
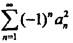绝对收敛。第3题：
A.k*exp(-k^2*x^2)/sqrt(pi);当k趋于无穷时
B.[1-cos(k*x)]/(pi*k*x^2);当k趋于无穷时
C.k/[pi*(1+k^2*x^2);当k趋于无穷时
D.sin(k*x)/(pi*x);当k趋于无穷时
第4题：
对于幂级数，其一般项系数开n次方后的极限为无穷大，则该幂级数发散。
第5题：
( )。
第6题：
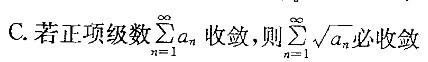
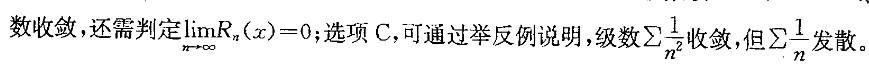
第7题：
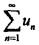收敛，则下列级数中不收敛的是（ ）。
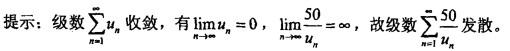
第8题：
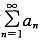收敛，则
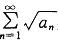必收敛
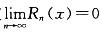；选项C，可通过举反例说明，级数
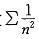收敛，但
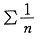发散。第9题：
当n趋于无穷时，级数的一般项的极限为0，则级数（）。
第10题：
正项数值级数收敛，则达朗贝尔判别法是：当n趋于无穷时（）。