泊松分布负指数分布CN
泊松分布泊松分布CN
负指数分布负指数分布NC
泊松分布负指数分布NC
第1题:
A、83.3%
B、75%
C、17%
D、50%
第2题:
设Xi (i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。
A.若Xi (i=1,2,…,n)服从正态分布,且分布参数相同,则 服从正态分布
服从正态分布
B.若Xi (i=1,2,…,n)服从指数分布,且λ相同,则 服从正态分布
服从正态分布
C.若Xi(i=1,2,…,n)服从[a,b)上的均匀分布,则 服从正态分布
服从正态分布
D.无论Xi (i=1,2,…,n)服从何种分布,其均值 都服从正态分布
都服从正态分布
第3题:
A.顾客到达间隔时间分布为泊松分布,服务时间为负指数分布,一个服务员
B.顾客到达间隔时间分布为任意分布,服务时间为负指数分布,m个服务员
C.顾客到达间隔时间分布为泊松分布,服务时间为定长分布,一个服务员
D.顾客到达间隔时间分布为任意分布,服务时间为定长分布,m个服务员
第4题:
Kendall符号中X/Y/Z各字母分别代表()。
第5题:
若到达排队系统的顾客为Poisson流,则依次到达的两名顾客之间的间隔时间服从负指数分布。
第6题:
设Xi(i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。
A.若Xi(i=1,2,…,n)服从正态分布,且分布参数相同,则 服从正态分布
服从正态分布
B.若Xi(i=1,2,…,n)服从指数分布,且λ相同,则 服从正态分布
服从正态分布
C.若Xi(i=1,2,…,n)服从[a,b]上的均匀分布,则 服从正态分布
服从正态分布
D.无论Xi(i=1,2,…,n)服从何种相同的分布,其均值 都服从正态分布
都服从正态分布
第7题:
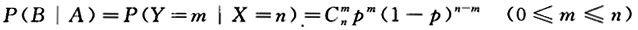
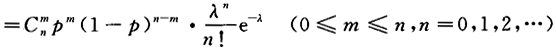
第8题:
第9题:
某服务部平均每小时有4个人到达,平均服务时间为6分钟。到达服从Poisson流,服务时间为负指数分布。由于场地受限制,服务部最多不能超过3人,求:顾客平均排队的时间
第10题:
若到达排队系统的顾客为泊松流,则依次到达的两名顾客之间的间隔时间服从负指数分布。