F分布
t分布
χ2分布
正态分布
第1题:
第2题:
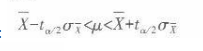
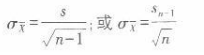

第3题:
A. 正态分布
B. F分布
C. t分布
D. χ2分
第4题:
对方差未知的正态总体进行样本容量相同的n次抽样,则这n个置信区间的宽度必然相等。
第5题:
第6题:
第7题:
 未知,则样本平均数的分布为( )
未知,则样本平均数的分布为( )
 分布
分布
 未知时,用样本的无偏方差(
未知时,用样本的无偏方差( )作为总体方差的估计值实现对总体平均数μ的估计。因为在总体方差未知时,样本平均数的分布为t分布,故应查t值表。故本题的正确答案是c。
)作为总体方差的估计值实现对总体平均数μ的估计。因为在总体方差未知时,样本平均数的分布为t分布,故应查t值表。故本题的正确答案是c。第8题:
A.总体方差已知且不等,n1和n2都是小样本容量
B.总体方差未知且相等,n1和n2都是大样本容量
C.总体方差未知且不等,n1和n2都是大样本容量
D.总体方差未知且相等,n1和n2都是小样本容量
第9题:
原总体为正态,总体方差未知且样本容量小于30情况下的平均数抽样分布为()
第10题:
设一正态总体N=200,平均数是40,对其进行样本容量为10的简单随机抽样,则平均数抽样分布的期望值是()。