y-z=0
2y+z=0
2y-z=0
y+z=0
第1题:
答案:不垂直于
解析:
平面一般力系的平衡条件:平面力系平衡的必要与充分条件是:力系的主矢量和力系对简化中心的主矩同时都为零
平面力系的平衡方程
根据主矢量和主矩的解析
表达式得
建立平面任意力系的二力矩式平衡方程应为:任意两点A、B为矩心列两个力矩方程,取x轴为投影轴列投影方程,但A、B两点的连线应不垂直于x轴。
第2题:
第3题:
曲线y=x3+1在点(1,2)处的切线方程是__________.
第4题:
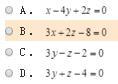

第5题:
第6题:


第7题:
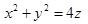




第8题:
曲线y=x2+1在点(1,2)处的切线方程为__________.
第9题:
第10题:
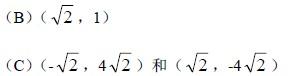
 。
。