第1题:
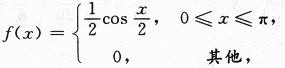
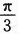 的次数,求Y^2的数学期望.
的次数,求Y^2的数学期望.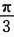 理解为试验成功,则Y表示独立地重复试验4次成功的次数,即Y~B(4,p)
理解为试验成功,则Y表示独立地重复试验4次成功的次数,即Y~B(4,p)
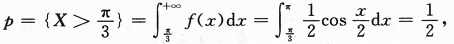

第2题:
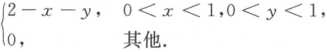 (1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
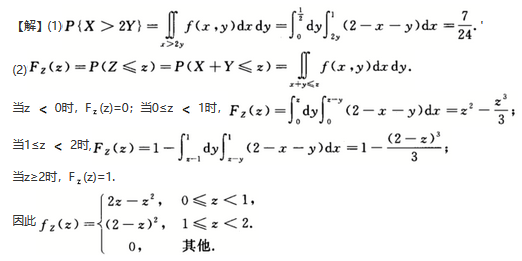
第3题:
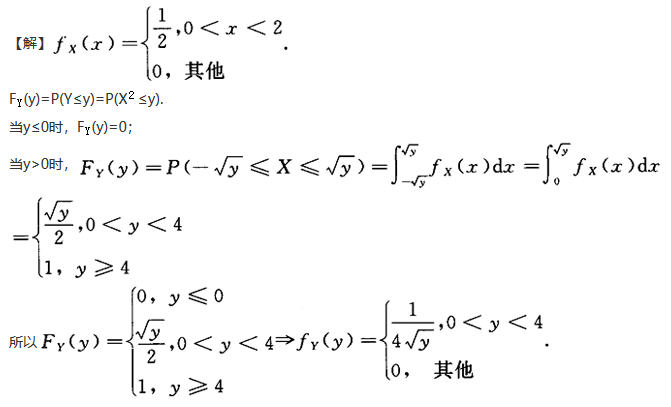
第4题:
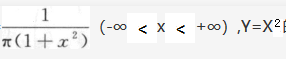 的概率密度为_______.
的概率密度为_______.
第5题:
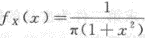 ,则y=2X的密度函数为
,则y=2X的密度函数为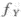 (y)=_______.
(y)=_______.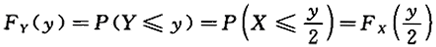 , 所以.
, 所以.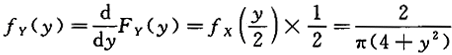
第6题:
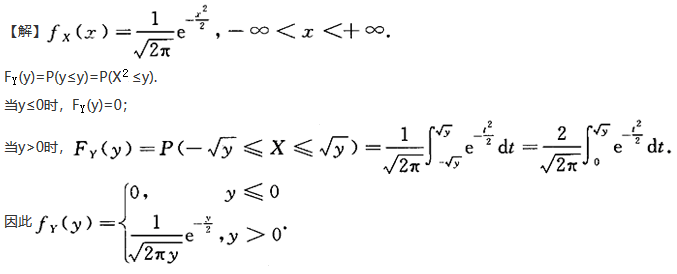
第7题:
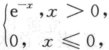 求y=e^x的概率密度FY(y).
求y=e^x的概率密度FY(y).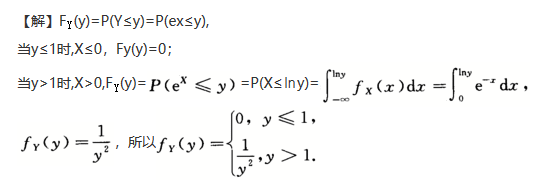
第8题:
 ,Y~E(4),令U=X+2Y,求U的概率密度.
,Y~E(4),令U=X+2Y,求U的概率密度.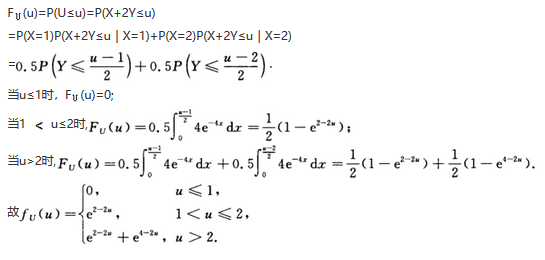
第9题:
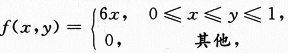 则P{X+Y≤1}=_______.
则P{X+Y≤1}=_______.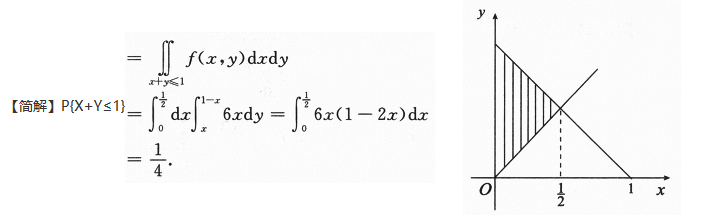
第10题:
