第1题：
已知数列{an}的前n项和Sn=n2-2n．求
（I）{an}的前三项；
（II）{an}的通项公式．
第2题：
设Sn为等差数列｛an｝的前n项和，若S3=3，S6=24，则a9= 。
第3题：
已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．
（I）求数列{an}的首项a1及通项公式；
（Ⅱ）数列{an}的前多少项的和等于847.
第4题：
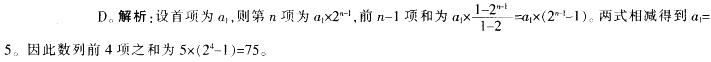
第5题：
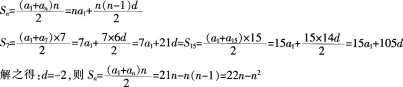
第6题：
已知数列{an}中,a1=2,an+1=(1+an)/(1-an).记数列{an}的前n项的乘积为∏n,则∏2012=____.
第7题：
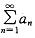收敛的什么条件？
第8题：
已知一个等差数列的首项为1，公差为3，那么该数列的前5项和为 （ ）
A.35
B.30
C.20
D.10
第9题：
两式相减得到a1 =3，因此数列前四项之和为3×（24-1）=45.第10题：