
第1题:
已知某个完全竞争行业中的单个厂商的短期成本函数是STC=0.1Q3—2Q2+15Q+10。求:
(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;
(2)当市场价格下降为多少时,厂商必须停产;
(3)厂商的短期供给函数。
第2题:
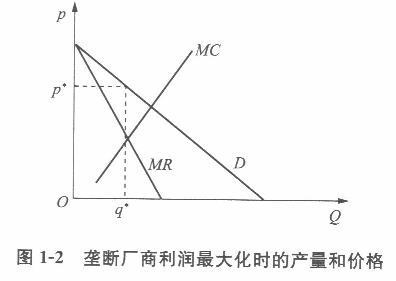
第3题:
计算题:
已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求:
(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;
(2)当市场上价格下降为多少时,厂商必须停产;
(3)厂商的短期供给函数
(1)根据MC=MR=P
MC=dSTC/dQ=0.3Q2-4Q+15=55=P
解得Q=20
利润=TR-STC=55*20-(0.1*203-2*202+15*20+10)=790
(2)停业点为AVC的最低点
AVC=TVC/Q=0.1Q2-2Q+15
当Q=10时AVC最小且AVC=5所以P=5时厂商必须停产
(3)短期供给函数即SMC函数且大于最低AVC对应产量以上的区间
SMC=dSTC/dQ=0.3Q2-4Q+15
所以短期供函数为0.3Q2-4Q+15(Q≥10)
第4题:


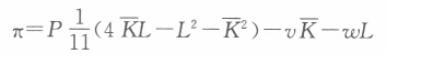
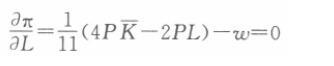
第5题:

第6题:

第7题:

第8题:
某成本不变的完全竞争行业的代表性厂商的长期总成本函数为LTC=Q3-60Q2+1500Q,产品价格P=975美元,市场需求函数为P=9600-2Q,
试求:
(1)利润极大时的产量、平均成本和利润。
(2)该行业长期均衡时的价格和厂商的产量。
(3)用图形表示上述(1)和(2)。
(4)若市场需求曲线是P=9600-2Q,试问长期均衡中留存于该行业的厂商人数是多少?
1)LMC=dLTC/dQ=3Q2-120Q+1500
当LMC=P=MR时,利润极大。
故,3Q2-120Q+1500=975,得Q1=5(舍);Q2=35
LAC=LTC/Q=Q2-60Q+1500=352+60×35+1500=625
π=TR-TC=P·Q-AC·Q=975×35-625×35=12250
(2)行业长期均衡时,LAC最小,当LAC′=0,且LAC〞>0时,有最小值。
即,(Q2-60Q+1500)′=2Q-60=0,得,Q=30,LAC〞=2>0
当Q=30时,P=LACmin=302-60×30+1500=600
(3)如图所示:


(4)若市场需求曲线是P=9600-2Q,又知长期均衡价格P=600,
业产量Q=(9600-P)/2=(9600-600)/2=4500
厂商人数N=行业产量/厂商产量=4500/30=150家
第9题:

第10题:
