第1题:
假定L单位的劳动力和K单位的资本相结合可以生产Q单位的产品,则生产函数可表示为Q=F(L,K),如果和L和K都增加X倍,产量为Q时,即当A=X时说明()
A.规模收益递减
B.规模收益不变
C.规模收益递增
D.不能确定
第2题:
生产函数Q=f(L,K)的要素组合与产量的对应图,如图所示,这张图是以坐标平面的形式编制的。其中,横轴和纵轴分别表示劳动投入量和资本投入量,虚线交点上的数字表示与该点的要素投入组合对应的产量。
(1)图中是否存在规模报酬递增、不变和递减?
(2)图中是否存在边际报酬递减?
(3)图中哪些要素组合处于同一条等产量曲线上?

(1)图中存在规模报酬递减与不变。如70=f(1,2)与130=f(2,4),此时生产要素增加比例为2,而产量增加比例为130/70,小于2,因此存在规模报酬递减。又如,50=f(1,1)与100=f(2,2)此时生产要素增加比例为2,而产量增加比例为100/50,等于2,因此存在规模报酬不变。
(2)图中存在边际报酬递减。如k=1保持不变,当L发生改变时,在0→1、1→2、2→3、3→4四段中,边际产量分别为50、20、10、5,可以看出边际报酬递减。
(3)f(2,1)与f(1,2)、f(3,1)与f(1,3)、f(4,1)与f(1,4)、f(3,2)与f(2,3)、f(4,2)与f(2,4)、f(4,3)与f(3,4)分别处于Q=70、Q=80、Q=85、Q=120、Q=130、Q=165等产量曲线上。
第3题:
此题为判断题(对,错)。
第4题:


第5题:
A.递增
B.递减
C.不变
D.先增后减
第6题:
已知某企业的生产函数Q=L2/3K1/3 ,劳动的价格W=2,资本的价格r=1,
求:
(1)当成本C=3000时,企业实现最大产量时的L、K和Q的值。
(2)当产量Q=800时,企业实现最少成本时的L、K和C的值。
如图:
L=800K=800 C=2L+K=3×800=2400
第7题:
已知生产函数Q=f(L,K)=2KL-0.5L2-0.5K2,假定厂商目前处于短期生产,且K=10,
求:
(1)写出在短期生产中该厂商关于劳动的总产量TPL函数、劳动的平均产量APL函数和劳动的边际产量MPL函数。
(2)分别计算当总产量TPL、劳动平均产量APL和劳动边际产量MPL各自达到极大值时的厂商劳动的投入量。(3)什么时候APL=MPL?它的值又是多少?
(1)短期生产中K是不变的,短期关于劳动的总产量函数为:
第8题:
计算题:假定某厂商只有一种可变要素劳动L,产出一种产品Q,固定成本为既定,短期生产函数Q=-0。1L3+6L2+12L,求:
(1)劳动的平均产量AP为最大值时的劳动人数
(2)劳动的边际产量MP为最大值时的劳动人数
(3)平均可变成本极小值时的产量
(1)因为:生产函数Q=-0.1L3+6L2+12L
所以:平均产量AP=Q/L=-0.1L2+6L+12
对平均产量求导,得:-0.2L+6
令平均产量为零,此时劳动人数为平均产量为最大。L=30
(2)因为:生产函数Q=-0.1L3+6L2+12L
所以:边际产量MP=-0.3L2+12L+12
对边际产量求导,得:-0.6L+12
令边际产量为零,此时劳动人数为边际产量为最大。L=20
(3)因为:平均产量最大时,也就是平均可变成本最小,而平均产量最大时L=30,所以把L=30代入Q=-0。1L3+6L2+12L,平均成本极小值时的产量应为:Q=3060,即平均可变成本最小时的产量为3060。
第9题:
已知可变要素劳动的短期生产函数的产量表如下:
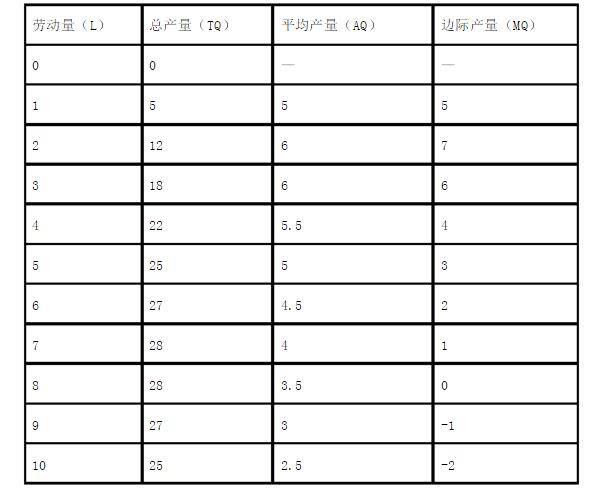
(1)计算并填表中空格
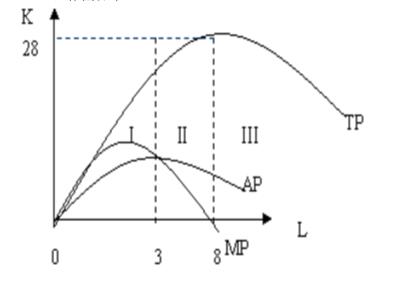
(2)在坐标图上做出劳动的总产量、平均产量和边际产量曲
(3)该生产函数是否符合边际报酬递减规律?
第10题:
