两个本原多项式g（x）和h（x）若在Q[x]中相伴，那么有什么等式成立？（）

第1题：

互素多项式的性质，（f（x），h（x））=1，（g（x），h（x））=1，则有（f（x）g（x），h（x））=1成立。

第2题：

一个次数大于0的本原多项式g（x）在Q上可约，那么g（x）可以分解成两个次数比g（x）次数低的本原多项式的乘积。

第3题：

若在区间(a，b)内，f′(x)=g′(x)则下列等式中错误的是( )。

A.f(x)=cg(x)
B.f(x)=g(x)+c
C.
D.df(x)=dg(x)

第4题：

两个本原多项式g（x）和h（x）若在Q[x]中相伴，那么有什么等式成立？（）

• A、g（x）=h（x）
• B、g（x）=-h（x）
• C、g（x）=ah（x）（a为任意数）
• D、g（x）±h（x）

第5题：

互素多项式的性质，若f（x）|g（x）h（x），且（f（x），g（x））=1，那么可以推出什么？（）

• A、g（x）
• B、h（x）
• C、f（x）g（x）
• D、f（x）

第6题：

在F（x）中，f（x），g（x）是次数≤n的多项式，若在F中有n+1个不同的元素，c1，c2…使得f（ci）=g（ci），则f（x）=g（x）。

第7题：

不可约多项式f（x）的因式有哪些？（）

• A、只有零次多项式
• B、只有零次多项式和f（x）的相伴元
• C、只有f（x）的相伴元
• D、根据f（x）的具体情况而定

第8题：

若在区间(a,b)内，f'(x)=g'(x)，则下列等式中错误的是：
A.f(x)=cg(x)
B.f(x)=g(x)+c

D. df(x)=dg(x)

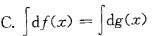
第9题：

互素多项式的性质，若f（x）|h（x），g（x）|h（x），且（f（x），g（x））=1，那么可以推出什么？（）

• A、f（x）g（x）
• B、h（x）
• C、h（x）
• D、g（x）

第10题：

在F[x]中，有f（x）+g（x）=h（x）成立，若将x用矩阵A代替，将有f（A）+g（A）≠h（A）。