第1题:
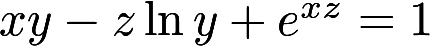 ,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程
,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程
第2题:
 所以dz=
所以dz=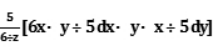
第3题:
(本题满分7分)设函数z=z(x,y)由方程x2+y2+z2=xyz确定,求δz/δy。

第4题:

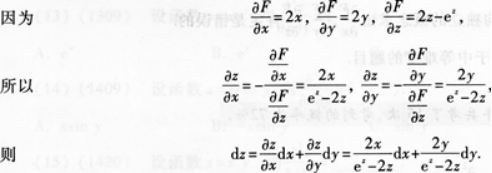
第5题:


第6题:

第7题:
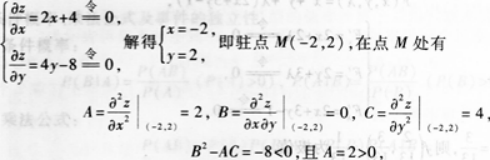
第8题:
(本题满分8分) 设函数z=z(x,y)是由方程x+y3+z+e2x=1所确定的隐函数,求dz.

第9题:
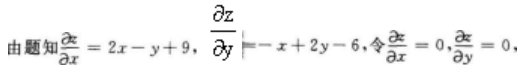
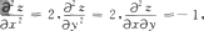
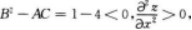
第10题:
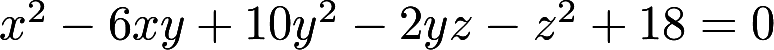 确定的函数,求
确定的函数,求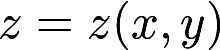 的极值点和极值
的极值点和极值