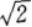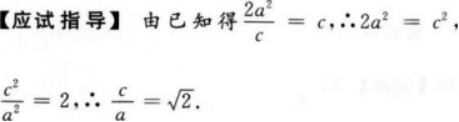双曲线题型归纳含(答案)

双曲线形的计算公式为(x2/a2)+(y2/b2)=1。()

本题答案：错

PT正常，APTT延长，见于下列缺乏的是

A、Ⅴ

B、Ⅶ

C、Ⅷ

D、Ⅱ

E、PF2

参考答案：C

F2812处理器的所有外设寄存器全部分组为外设帧PF0,PF1和PF2。这些帧都映射到处理器的数据区。()

此题为判断题(对，错)。

正确答案:正确

双曲线x2-y2/2 =1在点(-√2,√2)处的切线的方程是( ).

(A)y=-x+√2.

(B)y=-x+3√2.

(C)y=-2x-√2.

(D)y=-2x+3√2.

参考答案D

设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

A．2x-y+2=0
B．2x+y+1=0
C．2x+y-3=0
D．2x-y+3=0

答案：D

解析：

@##

摘要:资料三、典型例题选讲（一）考查双曲线的概念例1设P是双曲线x2y21上一点，双曲线的一条渐近线方程为3x2y0，F1、9a2F2分别是双曲线的左、右焦点．若|PF1|3，则|PF2|（）A．1或5B．6C．7D．9分析：根据标准方程写出渐近线方程，两个方程对比求出a的值，利用双曲线的定义求出|PF2|的值．解：双曲线3x2y21渐近线方程为y=x，由已知渐近线为3x2y0，2a9aa�2,||PF1||PF2||4，|PF2|4|PF1|.Q|PF1|3,|PF2|0，|PF2|7.故选C．归纳小结：本题考查双曲线的定义及双曲线的渐近线方程的表示法．（二）基本量求解例2(2009山东理)设双曲线点，则双曲线的离心率为（A．54B．5x2y221的一条渐近线与抛物线yx21只有一个公共2ab）C．52D．5b�b�yxx2y2解析：双曲线a，消去y，得1的一条渐近线为yx，由方程组�a2a2b2��yx1x2bbx10有唯一解，所以△=()240，aa所以bca2b2b2，e1()25，故选D．aaaa归纳小结：本题考查了双曲线的渐近线的方程和离心率的概念，以及直线与抛物线的位置.资料关系，只有一个公共点，则解方程组有唯一解．本题较好地考查了基本概念、基本方法和基本技能．例3（2009全国Ⅰ理）设双曲线+1相切，则该双曲线的离心率等于(A.3B.2C.5x2y21（a＞0，b＞0）的渐近线与抛物线y=x2a2b2)D.6解析：设切点P(x0,y0)，则切线的

已知双曲线C：x2/a2-y2/b2=1(a>0，b>0)的一个焦点是抛物线y2=8x的焦点，且双曲线C的离心率为2，那么双曲线C的方程为_______。

答案：

解析：